Hemmes mathematische Rätsel: Irische Geometrie in Frankreich
Die erste Ausgabe der französischen Mathematikzeitschrift »Nouvelles annales de mathématiques« wurde 1842 in Paris herausgegeben. Sie erschien 85 Jahre lang, bevor sie nach dem Ersten Weltkrieg 1927 eingestellt wurde. Die Zeitschrift enthielt eine Kolumne mit dem Titel »Questions«, in der Leser mathematische Aufgaben stellten, die auch oft aus dem Bereich der Unterhaltungsmathematik stammten. Im Jahr 1856 gab A. Burlet aus Dublin in Irland den Lesern folgendes Problem zu lösen, das hier geringfügig verändert worden ist.
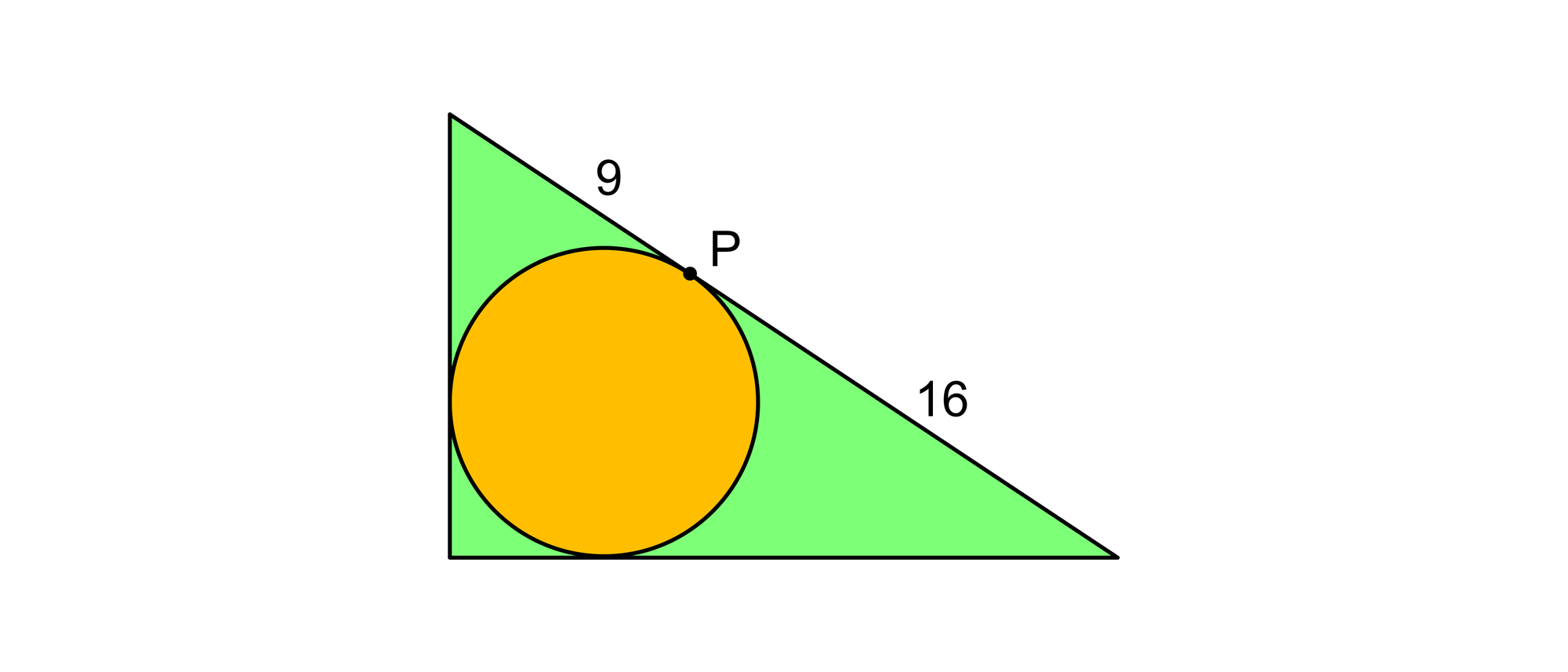
Der Inkreis eines rechtwinkligen Dreiecks berührt die Hypotenuse im Punkt P, und der Punkt P teilt die Hypotenuse in zwei Abschnitte, die 9 und 16 Einheiten lang sind. Wie groß ist Flächeninhalt des Dreiecks?
Der Mittelpunkt M des Inkreises wird mit den Ecken B und C des Dreiecks und mit den Berührpunkten P, Q und R seines Umfangs mit den Seiten verbunden. Dadurch wird das Dreieck in vier kleinere rechtwinklige Dreiecke und in ein Quadrat unterteilt.
Die Fläche F des Dreiecks ABC beträgt F = 1⁄2(a + r)(b + r). Die beiden Klammerausdrücke auf der rechten Gleichungsseite werden ausmultipliziert und man erhält F = 1⁄2(ab + r(a + b) + r2).
Die Fläche F kann man aber auch bestimmen, indem man die Flächen der vier kleinen Dreiecke und des Quadrats addiert. Dies ergibt F = 1⁄2ar + 1⁄2ar + 1⁄2br + 1⁄2br + r2, was zu F = r(a + b) + r2 zusammengefasst werden kann. Die zweite Gleichung wird jetzt in die erste eingesetzt. Dadurch erhält man F = 1⁄2(ab + F) oder F = ab.
Der Flächeninhalt des Dreiecks ist also das Produkt der beiden Hypotenusenabschnitte und hat somit die Größe 9 · 16 = 144.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.