»So, on behalf of the British government, and all those who live freely thanks to Alan's work I am very proud to say: we're sorry, you deserved so much better« – mit diesen Worten versuchte im Jahr 2009 der britische Premierminister Gordon Brown wieder gut zu machen, was dem englischen Mathematiker Alan Mathison Turing 55 Jahre zuvor widerfahren war. Die Postverwaltung der Karibikinsel St. Vincent ehrte Turing im Rahmen ihrer Milleniumsausgaben als eine der bedeutendsten Persönlichkeiten des 20. Jahrhunderts, ebenso die Post Portugals, während Großbritannien nur allgemein an die Fortschritte erinnerte, die mit der Erfindung des Computers verbunden sind.

Alan Turings Vater arbeitete als Angestellter der britischen Kolonialverwaltung in Indien; seine Mutter war in Indien geboren, wo ihr Vater als leitender Ingenieur bei der Madras-Eisenbahn beschäftigt war. Da die beiden ihre Kinder nicht in den unsicheren Verhältnissen Indiens aufwachsen lassen wollten, reiste die Mutter nach England, um dort ihren zweiten Sohn Alan zu gebären. Nach einem Jahr kehrte sie wieder nach Indien zurück, den Jungen sowie den älteren Bruder bei Freunden zurücklassend. Alan sah seine Eltern nur bei deren gelegentlichen Besuchen.

In den ersten Schuljahren fällt er als Schüler kaum auf. Als er mit 14 Jahren an eine 100 km entfernt liegende weiterführende Schule wechseln soll, ist sein Start in der Schule durch einen landesweiten Streik gefährdet. Um dennoch pünktlich dort zu sein, benutzt der wissensdurstige Jugendliche sein Fahrrad. Vom Unterricht an der neuen Schule enttäuscht, beschäftigt sich Alan Turing aber bald lieber mit eigenen Ideen.

In seiner Freizeit vertieft sich Alan Turing in Einsteins Relativitätstheorie und Eddingtons Veröffentlichungen zur Quantenmechanik, während er sich im Mathematikunterricht die Kritik seines Lehrers anhören muss, dass er bei seinen Lösungswegen nicht die vorgegebenen Methoden einhält. Gleichwohl gewinnt er alle ausgeschriebenen Mathematikwettbewerbe der Schule.

1931 wechselt er zum Mathematikstudium nach Cambridge, wo er endlich seinen eigenen Ideen folgen kann. Er ist fasziniert von John von Neumanns »Quantenmechanik« und von Bertrand Russells »Einführung in die mathematische Philosophie«. Zunehmend interessieren ihn Fragen der mathematischen Logik. Nach dem mit Auszeichnung bestandenen Bachelor-Examen belegt er einen Fortgeschrittenen-Kurs über die Grundlagen der Mathematik, der sich mit Gödels Entdeckungen zur Vollständigkeit und HilbertsEntscheidbarkeitsproblem auseinandersetzt. Hilbert hatte im Jahr 1900 unter anderem die Frage aufgeworfen: Gibt es einen Algorithmus, durch den für jede (ausreichend formalisierte) Aussage der Mathematik entschieden werden kann, ob diese wahr oder falsch ist? Wenn es einen solchen Algorithmus gibt, der dies leistet, dann kann man seine Existenz am einfachsten dadurch nachweisen, dass man ihn angibt. Wie aber soll man nachweisen, dass es keinen solchen Algorithmus gibt? Und wie soll ein solcher Nachweis aussehen, der ja selbst auch ein Algorithmus ist?

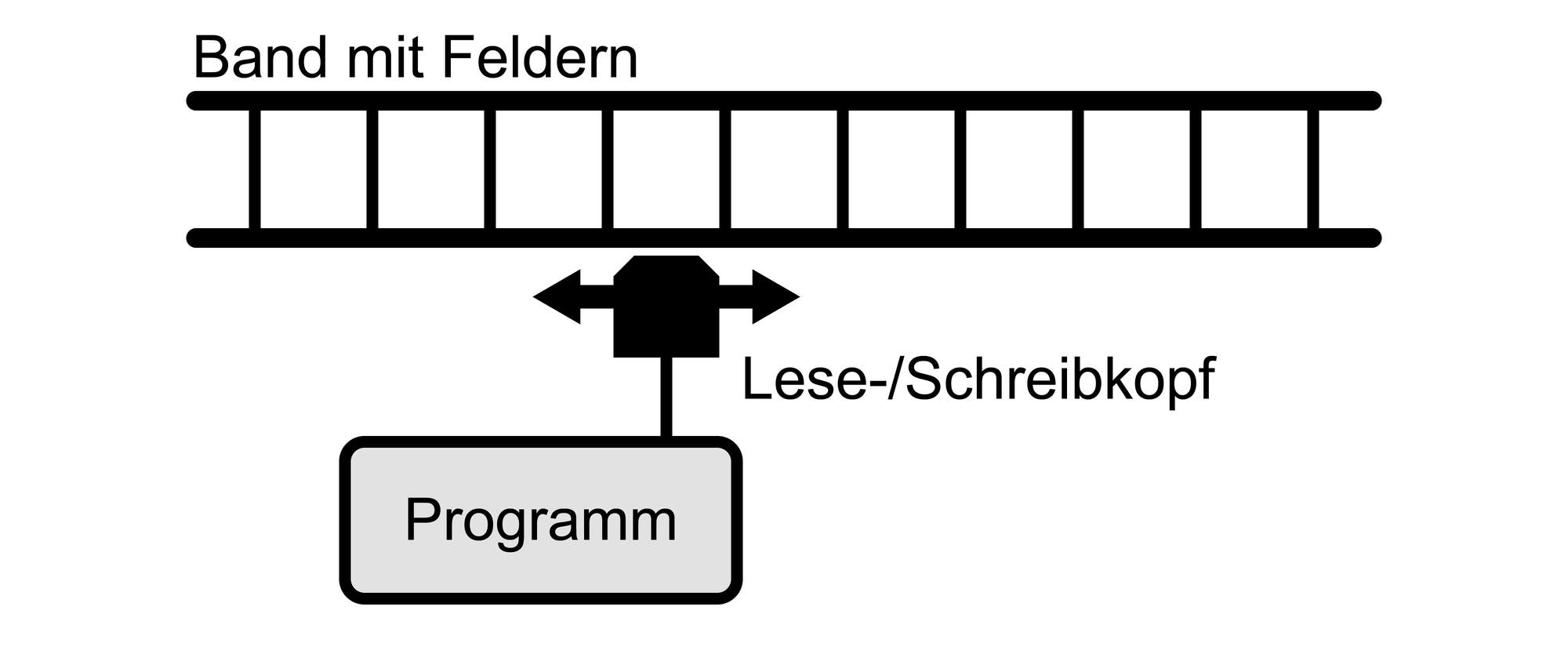
1936 verfasst Alan Turing, mittlerweile Fellow am King's College in Cambridge, den Beitrag On Computable Numbers with an application to the Entscheidungsproblem, in der er einen einfachen abstrakten Rechenautomaten beschreibt, der einer endlichen Menge von festen Regeln folgt. Diese heute so genannte Turing-Maschine beherrscht nur drei Operationen: lesen, schreiben und den Schreib-Lese-Kopf bewegen. Auf einem theoretisch unendlich langen Band aus Speicher-»Zellen« stehen Zeichen (aus einem endlichen Alphabet). Gemäß einem vorgegebenen Programm wird ein Zeichen gelesen oder überschrieben; dann bewegt sich der Schreib-Lese-Kopf um ein Feld nach links oder rechts oder hält an. Zahlen, die sich von einer solchen Maschine berechnen lassen – die Ziffern der Zahl werden schrittweise auf das ursprünglich leere Band geschrieben – bezeichnet er als berechenbar; beispielsweise zeigt er, dass \(\pi\) eine berechenbare Zahl ist.

Zu jeder berechenbaren Zahl lässt sich eine Turing-Maschine angeben; diese Turing-Maschinen sind natürlicherweise abzählbar. Daher gibt es auch nur abzählbar unendlich viele berechenbare Zahlen (wegen der Überabzählbarkeit der reellen Zahlen sind die meisten von ihnen in diesem Sinne also nicht berechenbar). Nach der Idee des cantorschen Diagonalverfahrens beschreibt er, welche Eigenschaften eine nicht berechenbare Zahl haben muss, und erkennt das Paradoxon, das darin liegt, dass er mit einer endlichen Anzahl von Regeln eine Zahl beschreibt, die nicht berechenbar ist, obwohl diese endliche Anzahl von Regeln ja selbst eine Turing-Maschine definiert. Das Problem liegt darin, dass es kein Verfahren gibt, mithilfe dessen man entscheiden kann, ob eine wie auch immer definierte Turing-Maschine den vorgegebenen Algorithmus zu Ende bringt oder nicht (Halte-Problem).

Dass seine fundamentalen Überlegungen nicht sogleich veröffentlicht werden, liegt darin begründet, dass Alonzo Church an der Princeton University einige Wochen zuvor einen Beitrag An unsolvable problem in elementary number theory eingereicht hat und einige der dort entwickelten Gedankengänge sich auch bei Turing finden. Turing ist gezwungen, in seinem Beitrag einen Hinweis auf den Aufsatz von Church zu ergänzen, um die historisch korrekte Abfolge zu dokumentieren, bevor sein Beitrag dann endlich erscheinen kann. In der Zwischenzeit ist er einer Einladung Churchs gefolgt und setzt seine Forschungen in Princeton fort.

Nach Cambridge zurückgekehrt, will er endlich eine Idee realisieren, die ihn seit der Entdeckung der Idee einer Turing-Maschine beschäftigt hat: der Bau eines realen Computers. Er denkt dabei nicht an ein elektronisches Gerät, so wie wir es heute kennen, sondern an eine analoge mechanische Einrichtung, die in der Lage ist, eine Liste von Anweisungen abzuarbeiten. Hierzu kommt es jedoch nicht: Er wird von der britischen Regierung gebeten, dabei mitzuhelfen, den Enigma-Code zu brechen. Als der Krieg ausbricht, wird die Arbeit des Teams von Wissenschaftlern in Blechtley Park strengster Geheimhaltung unterworfen; erst in den 1970er Jahren werden Einzelheiten hierüber bekannt.

Um 1930 hatten die militärischen Dienststellen in Deutschland damit begonnen, ihre Nachrichten mithilfe der Enigma (= griechisch: Rätsel) zu verschlüsseln, einer Maschine mit mehreren hintereinander geschalteten Walzen; hierdurch wurden die Buchstaben des Alphabets permutiert. Der Erfinder der Enigma unterlag jedoch bei der Konstruktion einem Trugschluss: Durch den zusätzlichen Einbau eines Umkehrrotors konnten die Walzen zwar doppelt zur Verschlüsselung genutzt werden, weil die Impulse vorwärts und rückwärts durch die Walzen liefen; hierdurch wurde aber die Anzahl der Möglichkeiten nicht erhöht, sondern verringert, da bei einer solchen Anordnung kein Zeichen in sich selbst permutiert werden kann – der Anteil der fixpunktfreien Permutationen beträgt nur circa 37 Prozent (= 1/e).

Den vom polnischen Geheimdienst angeworbenen Mathematikern Marian Rejewski, Henryk Zygalski und Jerzy Różycki gelang es bereits im Jahr 1933, eine elektromechanische Dechiffriermaschine zu bauen, mit der alle möglichen Walzenstellungen einer Enigma durchprobiert werden konnten. Sie nannten sie Bomba, nach einer beliebten Eissorte. Bei Kriegsausbruch gaben sie ihr Wissen an die Alliierten weiter. In der Zwischenzeit war die Enigma weiterentwickelt worden; die Walzen waren austauschbar, so dass der Zeitaufwand für die Entschlüsselung zunahm. Ende 1940 lässt Turing elektro-mechanische Maschinen bauen, mit der die verschlüsselten Funksprüche der deutschen Luftwaffe und Marine in kürzester Zeit entziffert werden können (Turing-»Bombe«) – nicht zuletzt dank seiner kriegsentscheidenden Idee, die Funksprüche statistischen Untersuchungen zu unterziehen. Die Arbeit wird schließlich durch den Bau eines ersten Computers mit über 2000 Röhren automatisiert (Colossus), an dessen Konzeption Turing ebenfalls maßgeblich beteiligt ist.

Nach Kriegsende wird Turing vom National Physical Laboratory in London eingeladen, an der Entwicklung einer Großrechenanlage (ACE = Automatic Computing Engine) mitzuarbeiten; insbesondere befasst er sich mit der Strukturierung der Programme für Großrechenanlagen. Seine zukunftsweisenden Ideen hinsichtlich der benötigten Speicherkapazitäten solcher Anlagen werden aber als überzogen beurteilt. Für einige Zeit nimmt er dann ein Angebot der Universität Manchester an (Projekt MADAM = Manchester Automatic Digital Machine). Seine sportlichen Ambitionen führen zu Spitzenplätzen bei nationalen Mittelstrecken- und Langstrecken-Meisterschaften.

1950 wird die Abhandlung Computing machinery and intelligence veröffentlicht, in der er sich mit den Fragen einer künstlichen Intelligenz beschäftigt und den – heute so genannten – Turing-Test entwickelt, durch den man entscheiden können soll, ob man es mit einem Mensch oder mit einer Maschine zu tun hat.

Seine Wahl zum Mitglied der Royal Society erfolgt 1951; der Schwerpunkt seiner Forschungsarbeiten liegt jetzt bei Fragen der theoretischen Biologie, nämlich wie Muster und Formen bei Lebewesen entstehen. Nach seinen Überlegungen entstehen Pigmente, beispielsweise Fellzeichnungen, dadurch, dass während der Embryonalentwicklung chemische Reaktionen mit unterschiedlichen Diffusionsgeschwindigkeiten ablaufen (The Chemical Basis of Morphogenesis, 1952).

Der kalte Krieg zwischen Ost und West führt dazu, dass wieder seine Forschungen der Geheimhaltung unterliegen. Als jemand versucht, ihn wegen homosexueller Beziehungen zu erpressen, wendet er sich an die Polizei, was ein Gerichtsverfahren zur Folge hat, bei dem er wegen Verstoßes gegen das gesetzliche Verbot homosexueller Beziehungen vor die Alternative gestellt wird, ins Gefängnis zu gehen oder sich einer Östrogenbehandlung zu unterziehen.

Seine Lebenssituation verschlechtert sich von da an dramatisch: Körperlich leidet der ambitionierte Sportler unter den Östrogen-Spritzen, gesellschaftlich ist die Ausgrenzung durch seine Umwelt spürbar, und nicht zuletzt bedrückt ihn die ständige Überwachung durch Sicherheitskräfte, in deren Augen er als Mitarbeiter an geheimen Projekten ein Sicherheitsrisiko darstellt. Auch leidet er darunter, dass seine Verdienste aus Geheimhaltungsgründen nicht bekannt werden, also eine allgemeine Anerkennung fehlt. Turing stirbt an einer Zyanidvergiftung, die nach Ergebnis einer gerichtlichen Untersuchung auf einen Selbstmord zurückzuführen ist.

In Würdigung seiner Verdienste verleiht die Association for Computing Machinery (ACM) seit 1966 in jedem Jahr den Turing-Award – die höchste Auszeichnung für Personen, die sich um die Entwicklung der Informatik verdient gemacht haben, vergleichbar etwa dem Nobelpreis oder der Fields-Medaille.