oder genauer ungerichteter Graph, ein Grundbegriff der Graphentheorie.

Ein Graph G besteht aus einer endlichen, nicht leeren Menge E(G) von Ecken und einer Menge K(G) von zweielementigen Teilmengen aus E(G). Man nennt E(G) Eckenmenge, |E(G)| Eckenzahl oder Ordnung, K(G) Kantenmenge und |K(G)| Kantenzahl des Graphen G.

Ein gerader bzw. ungerader Graph ist ein Graph gerader bzw. ungerader Ordnung. Ein Element k = {x, y} ∈ K(G) heißt Kante des Graphen G, und im allgemeinen wird die kurze und bequeme Schreibweise \begin{eqnarray}k=xy=yx\end{eqnarray} benutzt.

Zwei verschiedene Ecken x und y heißen adjazent, wenn es eine Kante k = xy gibt. Man sagt dann auch, die Kante k = xy inzidiert mit den Ecken x und y oder x und y sind durch die Kante k verbunden. Inzidieren zwei verschiedene Kanten mit einer gemeinsamen Ecke, so nennt man die Kanten inzident. Eine Ecke, die mit keiner Kante inzidiert, heißt isolierte Ecke. Im Fall K(G) = ∅ spricht man von einem leeren Graphen.

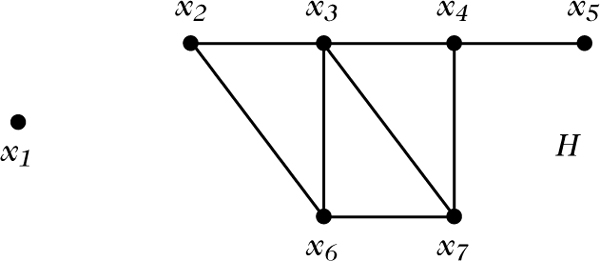
Falls ein Graph G nicht zu groß ist, so veranschaulicht man ihn sich am besten durch eine Skizze, indem man die Ecken als Punkte der Ebene und die Kanten als Verbindungslinien adjazenter Eckenpaare zeichnet. Die Abbildung zeigt einen Graphen H mit der Eckenmenge E(H) = {x₁, x₂, x₃, x₄, x₅, x₆, x₇} und den 8 Kanten x₂x₃, x₃x₄, x₄x₅, x₂x₆, x₃x₆, x₃x₇, x₄x₇, x₆x₇.

Der skizzierte Graph H besitzt folgende Eigenschaften. Er hat sieben Ecken, also ist |E(H)| = 7. Die Ecken x₂ und x₃ sind adjazent, und die Ecken x₂ und x₇ sind nicht adjazent. Die Kanten x₃x₄ und x₄x₇ sind inzident, die Kanten x₄x₅ und x₆x₇ sind nicht inzident. Der Graph H ist ungerade, und er besitzt die isolierte Ecke x₁.

Der Grad d_G(x) einer Ecke x in einem Graphen G zählt die mit x inzidenten Kanten. Man nennt \begin{eqnarray}\delta(G)=\min \{{d}_{G}(x)|x\,\in \,E(G)\}\end{eqnarray}

Minimalgrad und \begin{eqnarray}\Delta (G)=\max \{{d}_{G}(x)|x\,\in \,E(G)\}\end{eqnarray}

Maximalgrad von G. Die Zahl \begin{eqnarray}d(G)=\left(\displaystyle \sum _{x\in E(G)}{d}_{G}(x)\right)\,/|E(G)|\end{eqnarray} heißt Durchschnittsgrad von G.

Addiert man in einem Graphen G die Grade aller Ecken, so zählt man dabei jede Kante xy genau zweimal, nämlich einmal von x und einmal von y aus. Damit gelangt man zu der einfachen aber fundamentalen Identität \begin{eqnarray}\displaystyle \sum _{x\in E(G)}{d}_{G}(x)=2|K(G)|\end{eqnarray} von Leonhard Euler aus dem Jahre 1736, die auch unter dem Namen „Handschlaglemma“ bekannt ist. Als wichtige Folgerung ergibt sich daraus die Tatsache, daß die Anzahl der Ecken ungeraden Grades in einem Graphen stets gerade ist.

Eine endliche Folge von inzidenten Kanten \begin{eqnarray}W={x}_{0}{k}_{1}{x}_{1}{k}_{2}{x}_{2}\,\ldots \,{x}_{p-1}{k}_{p}{x}_{p},\end{eqnarray} mit k_i = x_i−1x_i ∈ K(G) für i = 1, 2,…,p heißt Kantenfolge von x₀ nach x_p der Länge p. Für W schreibt man auch kurz \begin{eqnarray}W={x}_{0}{x}_{1}\,\ldots \,{x}_{p}\,.\end{eqnarray}

Die Kantenfolge W ist geschlossen, wenn x₀ = x_p, und offen, wenn x0 ≠ x_p gilt.

Sind in einer Kantenfolge alle Kanten paarweise verschieden, so spricht man von einem Kantenzug, und sind sogar alle Ecken paarweise verschieden, so liegt ein Weg vor. Jede offene Kantenfolge von x₀ nach x_p enthält einen Weg von x₀ nach x_p. Ein geschlossener Kantenzug C = x₀k₁x₁…x_p−1k_px₀, in dem die Ecken x₀, x₁,…,x_p−1 paarweise verschieden sind, heißt Kreis.

In dem oben skizzierten Graphen H ist z. B. W = x₃x₂x₆x₃x₄x₇x₃ ein geschlossener Kantenzug der Länge 6, aber kein Kreis. Dagegen ist C = x₃x₂x₆x₇x₃ ein Kreis der Länge 4. Die Länge eines kürzesten Kreises in einem Graphen G ist die Taillenweite g(G) und die Länge eines längsten Kreises sein Umfang c(G). (Beide Werte seien ∞, wenn der Graph keinen Kreis besitzt.) Im skizzierten Graphen H gilt z. B. g(H) = 3 und c(H) = 5. Ist δ(G) ≥ 2, so hat G.A. Dirac 1952 gezeigt, daß G einen Kreis besitzt und c(G) ≥ δ(G) + 1 ist.

Haben alle Ecken eines Graphen G den gleichen Grad, so heißt G regulär. Ein regulärer Graph vom Grad 3 wird auch kubisch genannt. Da die Anzahl der Ecken ungeraden Grades stets gerade ist, muß ein kubischer Graph ein gerader Graph sein. Ein Graph der Ordnung n, in dem jedes Paar von Ecken adjazent ist, heißt vollständiger Graph, in Zeichen K_n. Ein vollständiger Graph K_n ist regulär, und er besitzt n(n−1)/2 Kanten. Der Komplementärgraph \(\bar{G}\) eines Graphen G besteht aus der Eckenmenge E(G), und in \(\bar{G}\) sind zwei Ecken genau dann adjazent, wenn sie es in G nicht sind.

Zur Darstellung von Graphen, z. B. in einem Computer, eignen sich besonders gut die sogenannten Adjazenz- und Inzidenzmatrizen. Es sei G ein Graph mit der Eckenmenge {x₁, x₂,…,x_n} und der Kantenmenge {k₁, k₂,…,k_m}. Die quadratische (n × n)-Matrix A_G = ((a_ij)) mit a_ij = 1, falls x_ix_j ∈ K(G) und a_ij = 0, falls x_i und x_j nicht adjazent sind, heißt Adjazenzmatrix. Die (n×m)-Matrix I_G = ((b_ij)) mit b_ij = 1, falls x_i und k_j inzident sind und b_ij = 0, falls x_i und k_j nicht inzident sind, wird Inzidenzmatrix oder Inzidenzliste genannt.

Numeriert man die Ecken eines Graphen G der Ordnung n mit den Zahlen {1, 2,…,n}, so spricht man von einem numerierten oder markierten Graphen der Ordnung n. Dabei werden zwei markierte Graphen mit der gleichen numerierten Eckenmenge {1, 2,…,n} genau dann als verschieden angesehen, wenn zwei Ecken i ≠ j existieren, die in dem einen Graphen adjazent, in dem anderen jedoch nicht adjazent sind. Man kann nun recht einfach zeigen, daß es genau 2ⁿ(n^−1)/2 markierte Graphen der Ordnung n gibt.