Lexikon der Mathematik: Raum-Zeit-Kontinuum
kurz Raum-Zeit genannt, die vierdimensionale Pseudo-Riemannsche Mannigfaltigkeit der Relativitätstheorie. Ihre Elemente heißen Ereignisse.
Die Beziehung zur klassischen Physik besteht in folgendem: Nach Einführung eines Bezugssystems läßt sich, zumindest lokal, eine (3 + 1)-Zerlegung der Raum-Zeit vornehmen, wobei dort Koordinaten xi, i = 0, … 3, verwendet werden. Dann ist x0 der Zeitpunkt, und der xα, α = 1, 2, 3 der Ort des Ereignisses.
Eine Pseudo-Riemannsche Mannigfaltigkeit ist hierbei dasselbe wie eine Riemannsche Mannigfaltigkeit, mit dem einzigen Unterschied, daß der metrische Tensor nicht positiv definit, sondern von Lorentz-Signatur (+, −,…,−) ist.
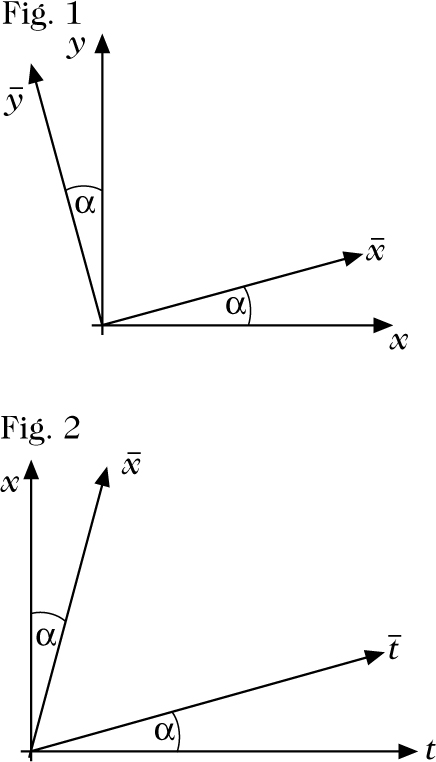
Vergleich von Drehung (Fig. 1) und Lorentz-Drehung (Fig. 2)
Der Unterschied der Signaturen wird schon in der zweidimensionalen Veranschaulichung deutlich: Figur 1 stellt die Euklidische Ebene in kartesischen Koordinatenachsen x, y dar. Werden diese um den Winkel α gedreht, entstehen die Koordinatenachsen \(\bar{x},\bar{y}\). Hier sind beliebige Drehwinkel α möglich, die Drehgruppe ist kompakt. Figur 2 stellt dieselbe Situation in der Raum-Zeit mit Zeitachse t und Raumachse x dar, hier ist der gezeichnete Winkel α ein Maß für die Geschwindigkeit, mit der sich das Bezugssystem (t, x) gegen das Bezugssystem \((\bar{t},\bar{x})\) bewegt. Es ist zu bemerken, daß schon qualitativ ein Unterschied zur normalen Drehung besteht, was die gegenseitige Lage der Achsen betrifft. Wenn α gegen der Wert 45° konvergiert, ergibt sich im Grenzfall keine zulässige Transformation mehr, da dann beide Achse parallel werden.
Physikalisch entspricht dieser Grenzfall einer Bewegung mit Lichtgeschwindigkeit, die im Rahmen der Relativitätstheorie nur beliebig angenähert, nicht aber erreicht werden kann. Mathematisch besteht der Unterschied zwischen beiden Figuren darin, daß die Lorentz-Gruppe nicht kompakt ist.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.