B. Lenze

Im Rahmen der Theorie und Anwendung (künstlicher oder formaler) neuronaler Netze wird versucht, einige wesentliche Mechanismen realer neuronaler Strukturen so zu formalisieren, daß die entstehenden Paradigmen in verschiedenen Gebieten einsetzbar sind und zu neuen Einsichten oder Techniken führen (exemplarisch seien genannt: Biologie, Physik, Informatik, Mathematik). Aus der speziellen Sicht der Mathematik kann man den Begriff des neuronalen Netzes am besten über die Graphentheorie einführen, zumindest was die primäre Topologie des Netzes betrifft:

Es sei G ≔ (X, H, γ) ein schlichter gerichteter Graph mit einer endlichen nichtleeren Eckenmenge X, einer endlichen Kantenmenge H mit H ∩ X = ∅ und einer Inzidenzabbildung γ : H → X × X. Ferner möge für alle Ecken v ∈ X mit δ⁺(v) der Außen- oder Ausgangsgrad und mit δ⁻ (v) der Innen- oder Eingangsgrad von v bezeichnet sein. Definiert man nun die Mengen \(\tilde{X}\subset X\)und \(\tilde{H}\subset H\)als

\begin{eqnarray}\begin{array}{c}\tilde{X}:=X\backslash \{v\in X|{\delta }^{+}(v)\cdot {\delta }^{-}(v)=0\},\\ \tilde{H}:=H\backslash \{h\in H|\gamma (h)\in (X\backslash \tilde{X})\times (X\backslash \tilde{X})\},\end{array}\end{eqnarray}

\begin{eqnarray}N:=(X,\tilde{X},H,\tilde{H},\gamma ),\end{eqnarray}

Ferner sind folgende Bezeichnungen üblich:

• Alle Elemente \(v\in \tilde{X}\)heißen Knoten von N.
• Alle Elemente \(h\in \tilde{H}\)heißen Vektoren von N.
• Alle Knoten \(v\in \tilde{X}\), für die ein \(w\in X\backslash \tilde{X}\)und ein \(h\in \tilde{H}\)existiert mit der Eigenschaftγ(h) = (w, v), heißen Eingangsknoten von N. Der Vektor \(h\in \tilde{H}\)wird dann Eingangsvektor von N genannt. Besitzt N keine Eingangsknoten und -vektoren, dann wird N eingangsloses neuronales Netz genannt.
• Alle Knoten \(v\in \tilde{X}\), für die ein \(w\in X\backslash \tilde{X}\)und ein \(h\in \tilde{H}\)existiert mit der Eigenschaftγ(h) = (v, w), heißen Ausgangsknoten von N. Der Vektor \(h\in \tilde{H}\)wird dann Ausgangsvektor von N genannt. Besitzt N keine Ausgangsknoten und -vektoren, dann wird N ausgangsloses neuronales Netz genannt.
• Besitzt der N induzierende schlichte gerichtete Graph G keine geschlossenen gerichteten Pfade, dann nennt man N (neuronales) Feed-Forward-Netz oder vorwärtsgerichtetes oder vorwärtsgekoppeltes (neuronales) Netz. Ansonsten nennt man N (neuronales) Feed-Back-Netz oder rekursives oder rückgekoppeltes (neuronales) Netz.

Einige erklärende Worte zur obigen Definition, wobei im folgenden keine ein- oder ausgangslosen neuronalen Netze betrachtet werden: Zunächst ist klar, daß die Knotenmenge \(\tilde{X}\) und die Vektorenmenge \(\tilde{H}\) durch verschiedene schlichte (d. h. schlingen- und mehrfachkantenfreie) gerichtete Graphen G erzeugbar ist. Im allgemeinen gibt es aber einen naheliegenden Graph mit einer minimalen Anzahl von Ecken und Kanten, der dann üblicherweise kanonisch als Erzeuger fixiert wird.

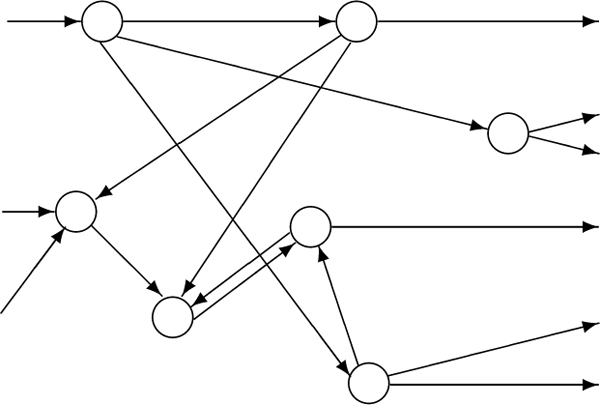
Die Knotenmenge \(\tilde{X}\) besteht genau aus den Ecken des gerichteten Graphen G, die sowohl Anfangsecken als auch Endecken sind. Salopp gesprochen sind dies Ecken, die wegen der Schlingen- freiheit sowohl erreichbar sind, als auch wieder verlassen werden können. Alle Ecken v ∈ X, die nur Anfangsecken, nur Endecken oder sogar nur isolierte Ecken sind, werden entfernt. Schließlich werden auch noch alle Kanten entfernt, die reine Anfangsecken mit reinen Endecken verbinden und nach Entfernung dieser Ecken keinen Bezug mehr zu den verbleibenden Ecken bzw. Knoten in \(\tilde{X}\) hätten. Dies führt zur Menge \(\tilde{H}\). Es ist natürlich klar, daß alle Ecken aus \(X\backslash \tilde{X}\) und alle Kanten aus \(H\backslash \tilde{H}\) auch nicht mehr skizziert werden, wenn es darum geht, sich die Topologie eines neuronalen Netzes zu veranschaulichen. Diese spielen nämlich in Hinblick auf die noch zu definierende Dynamik neuronaler Netze auch absolut keine Rolle mehr. Lediglich die Knoten aus \(\tilde{X}\) und die Vektoren aus \(\tilde{H}\) sind relevant (vgl. Abbildung).

Im folgenden wird motiviert, warum man gewisse Ecken und Kanten entfernt, um zum Konzept formaler neuronaler Netze zu kommen. Dazu betrachtet man einen beliebigen Knoten v in einem neuronalen Netz N. Für ihn gilt

\begin{eqnarray}{\delta }^{+}(v)\cdot {\delta }^{-}(v)\ne 0,\end{eqnarray}

Konkret läßt sich die Funktionsweise eines solchen Netzes nun wie folgt beschreiben: Über die Eingangsvektoren von N erhalten zunächst die in den Eingangsknoten von N angesiedelten Neuronen (im folgenden auch Eingangsneuronen oder Eingabe-Neuronen genannt) gewisse Eingabewerte, die diskret oder kontinuierlich sein können. Diese verarbeiten die Information im Sinne formaler Neuronen und geben sie über die auf ihnen beginnenden Vektoren, die nun auch Verbindungen, Links oder ( formale) Synapsen genannt werden, ins Netz weiter. Dabei ist es in vielen Fällen notwendig, die Knoten bzw. Neuronen des Netzes durchzunumerieren, um so festzulegen, in welcher Reihenfolge welche (Mengen von) Neuronen aktiv werden (Aspekt sequentiell/parallel).

Ferner ergänzt man i. allg. die Funktionalität der formalen Neuronen durch einen lokalen Speicher, in den das jeweilige Neuron ihm zugängliche Informationen ablegen kann und auf den es bei Bedarf gemäß einer gewissen Systematik zugreifen kann, um sein Ausgabeverhalten zu modifizieren. Man spricht in diesem Kontext (sequentielle/parallele Aktualisierung und lokaler Speicher) von Scheduling oder Signalflußkontrolle. Ist eine derartige Vorschrift gegeben, kann man über die Ausgangsknoten (bzw. Ausgangsneuronen oder AusgabeNeuronen) des Netzes (eventuell nach Verstreichen einer gewissen Zeit) die Reaktion des Netzes auf die primären Eingabewerte abgreifen. Berücksichtigt man all diese Randbedingungen, dann ist abbildungstheoretisch ein neuronales Netz N mit formalen Neuronen in den Knoten und vorgegebenem Scheduling nichts anderes als die spezielle Realisierung einer Funktion \({\mathcal{N}}\),

\begin{eqnarray}{\mathcal{N}}:{{\mathbb{R}}}^{n}\to {{\mathbb{R}}}^{m},\end{eqnarray}

\begin{eqnarray}{\mathcal{N}}:Abb({{\mathbb{R}}}^{k},{{\mathbb{R}}}^{n})\to Abb({{\mathbb{R}}}^{k},{{\mathbb{R}}}^{m}),\end{eqnarray}

Es sei mit Nachdruck darauf hingewiesen, daß in der Literatur begrifflich häufig nicht zwischen der Topologie eines neuronalen Netzes N und seiner endgültigen anwendbaren Realisierung im Sinne der Funktion \({\mathcal{N}}\) unterschieden wird: Beides wird neuronales Netz oder kurz Netz genannt, und aus dem jeweiligen Kontext ist i. allg. leicht zu entnehmen, in welchem Sinne der Begriff benutzt wird. Desweiteren ist es in vielen Fällen unmöglich, die Funktion \({\mathcal{N}}\) in lesbarer geschlossener Form darzustellen; in diesen Fällen entwickelt man die Wirkung des Netzes auf eine konkrete Eingabe Schritt für Schritt dem jeweiligen Scheduling folgend.

Ferner sei erwähnt, daß die oben skizzierte deterministische Dynamik im Kontext sogenannter probabilistischer neuronaler Netze durch stochastische Komponenten ergänzt oder vollständig ersetzt wird und dann natürlich auch in ein wahrscheinlichkeitstheoretisches Kalkül eingebettet werden muß.

Insgesamt beschreibt die bisher diskutierte Dynamik lediglich den sogenannten Ausführ-Modus eines neuronalen Netzes. Dieser ist natürlich erst dann sinnvoll einsetzbar, wenn das Netz zuvor in einem sogenannten Lern-Modus unter Anwendung einer Lernregel so konfiguriert wird, daß es in angemessener Weise auf gegebene Eingabewerte reagieren kann. Der Lern-Modus dient also der Einstellung der Parameter eines Netzes bzw. seiner formalen Neuronen in Abhängigkeit von einer gegebenen Problemstellung, wobei im Extremfall im Rahmen eines Lernprozesses sogar gestattet sein kann, daß die Topologie des primären Netzes verändert wird.

Grundsätzlich unterscheidet man zwischen überwachtem und unüberwachtem Lernen. Überwachtes Lernen liegt vor, wenn der Lernregel diskrete oder kontinuierliche Trainingswerte

\begin{eqnarray}({x}^{(s)},{y}^{(s)})\in {{\mathbb{R}}}^{n}\times {{\mathbb{R}}}^{m}\end{eqnarray}

\begin{eqnarray}({x}^{(s)},{y}^{(s)})\in Abb({{\mathbb{R}}}^{n}\times {{\mathbb{R}}}^{m})\times Abb({{\mathbb{R}}}^{k},{{\mathbb{R}}}^{m}),\end{eqnarray}

Im Unterschied dazu spricht man von unüberwachtem Lernen, wenn der Lernregel lediglich diskrete oder kontinuierliche Trainingswerte x^(s) ∈ ℝⁿ bzw. x^(s) ∈ Abb(ℝ^k, ℝⁿ), 1 ≤ s ≤ t, für die Eingabe zur Verfügung stehen und ohne Kenntnis der zugehörigen korrekten Ausgabewerte eine Adaption der Netzparameter (ggfs. bis hin zur Netztopologie) vorgenommen werden muß. Generelles Ziel beim unüberwachten Lernen ist es im allgemeinen, dafür zu sorgen, daß die Netzparameter so justiert werden, daß in irgendeinem Sinne ähnliche Eingabewerte auch zu ähnlichen oder sogar identischen Ausgaben des Netzes führen, d.h. \(x\approx \tilde{x}\Rightarrow {\mathcal{N}}(x)\approx {\mathcal{N}}(\tilde{x})\) bzw. \(x\approx \tilde{x}\Rightarrow {\mathcal{N}}(x)\approx {\mathcal{N}}(\tilde{x})\). In Hinblick auf konkrete Realisierungen für unüberwachtes Lernen sei verwiesen auf: adaptive-resonance-theory, Kohonen-Lernregel oder Oja-Lernregel.

Erwähnt sei abschließend wieder, daß es sowohl für überwachtes als auch für unüberwachtes Lernen neben den deterministischen Varianten auch stochastische Realisierungen gibt, die dann wieder in einen wahrscheinlichkeitstheoretischen Kalkül eingebettet werden.

Schließlich gibt es auch einige Implementierungen neuronaler Netze, bei denen keine eindeutige Trennung zwischen Ausführ- und Lern-Modus möglich ist, sondern Lernen und Ausführen ineinander übergehen. In diesem Zusammenhang und in Hinblick auf weitere Details sei auf die folgende Literatur verwiesen.

[2] Hecht-Nielsen, R.: Neurocomputing. Addison-Wesley Reading Massachusetts, 1990.

[3] Hoffmann, N.: Kleines Handbuch Neuronale Netze. Vieweg Verlag Braunschweig-Wiesbaden, 1993.

[4] Kamp, Y.; Hasler, M.: Recursive Neural Networks for Associative Memory. Wiley Chichester, 1990.

[5] Kohonen, T.: Self-Organization and Associative Memory. Springer Verlag Berlin, 1984.

[6] Lenze, B.: Einführung in die Mathematik neuronaler Netze. Logos Verlag Berlin, 1997.

[7] Minsky, M.; Papert, S.: Perceptrons. MIT Press Cambridge Massachusetts, 1969.

[8] Müller, B.; Reinhardt, J.: Neural Networks. Springer Verlag Berlin, 1991.

[9] Rojas, R.: Theorie der neuronalen Netze. Springer Verlag Berlin, 1993.

[10] Rumelhart, D.E.; McClelland, J.L.: Parallel Distributed Processing: Explorations in the Microstructure of Cognition Vol. I&II. MIT Press Cambridge Massachusetts, 1986.

[11] Schalkoff, R.J.: Artificial Neural Networks. McGraw-Hill New York, 1997.

[12] Zell, A.: Simulation Neuronaler Netze. Addison-Wesley Bonn, 1994.