Lexikon der Chemie: Rotationsspektren
Rotationsspektren, Molekülspektren, die auf einer Anregung von Molekülrotationen beruhen. Sie werden im fernen Infrarot (Infrarotspektroskopie) und im Mikrowellengebiet Mikrowellenspektroskopie) beobachtet und liefern vornehmlich Aussagen zur Molekülstruktur.
Theoretische Grundlagen. Moleküle führen bei entsprechender Energiezufuhr Rotationen um die Hauptträgheitsachsen aus. Da die Rotationsenergie gequantelt ist, können nicht beliebige, sondern nur ganz bestimmte Rotationsenergien auftreten, die in diskreten Energiezuständen des Rotators zum Ausdruck kommen. Nach der Quantentheorie sind nur solche Rotationsenergien Erot möglich, die der Gleichung
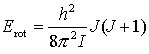
(1)
entsprechen. I bedeutet das Trägheitsmoment des Moleküls bezüglich der entsprechenden Drehachse, J die Rotationsquantenzahl, die die Werte 0, 1, 2, 3 ... annehmen kann, und h das Plancksche Wirkungsquantum. Beim Übergang von einem niederen Energiezustand in einen höheren absorbiert das Molekül die Energiedifferenz in Form elektromagnetischer Strahlung. Voraussetzung dafür ist, daß das betreffende Molekül ein permanentes Dipolmoment aufweist, da nur dann eine Wechselwirkung mit elektromagnetischer Strahlung möglich ist.
Der geometrische Bau des Moleküls, der sich im Trägheitsmoment widerspiegelt, bestimmt weitgehend das Aussehen der Rotationsspektren. Lineare Moleküle, die durch ein einziges Trägheitsmoment charakterisiert werden, und symmetrische Kreiselmoleküle (d. s. Moleküle mit einer drei- oder mehrzähligen Symmetrieachse, z. B. CH3Br, in denen zwei der Hauptträgheitsmomente gleich sind) zeigen verhältnismäßig einfache Rotationsspektren, bestehend aus Linien mit nahezu äquidistantem Abstand. Dagegen weisen asymmetrische Kreiselmoleküle (d. s. Moleküle mit einer zweizähligen Symmetrieachse oder geringerer Symmetrie) sehr linienreiche, komplizierte R. auf, die schwierig zu analysieren sind. Es wird deshalb nur der einfachste Fall eines zweiatomigen Moleküls näher betrachtet, dessen Rotationseigenschaften sich durch das Hantelmodell (Abb. 1a) beschreiben lassen, in dem sich die beiden Atome A und B in einem festen Abstand r1 zueinander befinden. Zur weiteren Vereinfachung kann man das Hantelmodell durch das Modell des starren Rotators ersetzen, in dem eine Masse
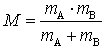
um eine feste Achse im Abstand r rotiert (Abb. 1b).
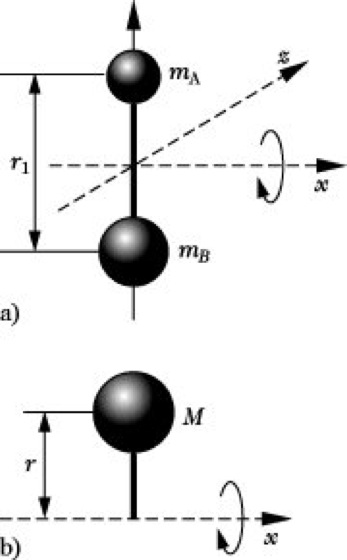
Rotationsspektren. Abb. 1: Modell der rotierenden Hantel (a) und des starren Rotators (b).
Für Gl. 1 schreibt man in der Molekülspektroskopie
Erot= h·c·B·J(J + 1), (2)
wobei die Rotationskonstante
eine für jedes Molekül charakteristische Größe ist (c = Lichtgeschwindigkeit). Sie kann direkt aus dem Spektrum entnommen werden und hat die Dimension einer Wellenzahl (cm-1). Trägt man die sich nach Gl. 2 ergebenden Termwerte, d. s. die durch h·c dividierten Energiewerte, graphisch auf, so erhält man das in Abb. 2 dargestellte Termschema, in dem rechts die Rotationsquantenzahl J, links die Termwerte in Einheiten von B angeschrieben sind. Jede Absorptionslinie im Spektrum entspricht einem definierten Termübergang, wobei in Absorption die Auswahlregel ΔJ = +1 gilt. Dabei ist zu beachten, daß die Molekülrotationen bei Zimmertemperatur schon durch die Übertragung thermischer Energie angeregt sind, so daß die Absorptionen nicht nur vom Rotationsgrundzustand J= 0, sondern auch von höheren Rotationszuständen aus erfolgen können, wie das auch im Termschema dargestellt ist. Es ergeben sich eine Reihe äquidistanter Rotationslinien (Abb. 2) den Wellenzahlen 2 B, 4 B, 6 B, 8 B .... d. h. jeweils im Abstand 2 B voneinander. Derartige R. werden an zweiatomigen Molekülen wie den Halogenwasserstoffen tatsächlich gefunden. Ein genaues Ausmessen der R. zeigt, daß die Linien nicht völlig gleiche Abstände haben, sondern mit größer werdender Rotationsquantenzahl J enger zusammenrücken. Das liegt daran, daß bei hoher Rotationsanregung die auftretende Zentrifugalkraft den Abstand der Atome schon merklich vergrößert, wodurch sich das Trägheitsmoment und somit nach Gl. 2 auch das Erot verändert. Die Behandlung des Moleküls als starrer Rotator ist nur für niedriges J zulässig. Bei zweiatomigen Molekülen sind die Rotationen um die x- und die z-Achse (Abb. 1a) energetisch gleichwertig, so daß sie zu dem gleichen Spektrum führen. Eine Anregung um die y-Achse ist wegen des bezüglich dieser Achse kleinen Trägheitsmomentes nicht möglich, wodurch das R. zweiatomiger Moleküle sehr einfach ist. Für mehratomige Moleküle geringer Symmetrie sind die Rotationsenergien um die Hauptträgheitsachsen nicht mehr äquivalent, so daß kompliziertere Spektren entstehen.

Rotationsspektren. Abb. 2: Rotationstermschema.
Probenpräparation und Aufnahmetechnik. Die Untersuchung von R. ist nur im gasförmigen Zustand möglich. Zur Ausschaltung zwischenmolekularer Wechselwirkungen wird bei möglichst geringem Druck (etwa 1 bis 100 Pa) gearbeitet. Unter Verwendung von Hochtemperaturzellen, mit denen sich Temperaturen bis 1000 °C erreichen lassen, können praktisch alle Substanzen vermessen werden, die sich unzersetzt verdampfen lassen. R. werden mit zwei verschiedenen Aufnahmetechniken vermessen. Der kurzwellige Teil wird mit optischen Spektrometern (Spektralapparaturen) untersucht, der langwellige Teil fällt in den Bereich der Mikrowellen und wird durch die Hochfrequenztechnik erfaßt. Nach Gl. 1 und 2 absorbieren Moleküle mit kleinem Trägheitsmoment, z. B. Fluorwasserstoff, im fernen Infrarot, Moleküle mit großem Trägheitsmoment im Mikrowellenbereich.
Anwendung der R. Analytik.Da die Spektren durch Rotation des Gesamtmoleküls um die Trägheitsachsen zustande kommen, ist das R. charakteristisch für das Molekül als ganzes und kann zu dessen Identifizierung benutzt werden, sofern ein an einer authentischen Probe erhaltenes Vergleichsspektrum zur Verfügung steht. Da unter den Meßbedingungen keine zwischenmolekularen Wechselwirkungen auftreten, können auch Substanzgemische untersucht werden. Infolge des hohen Auflösevermögens werden z. B. im Methylchlorid zwei verschiedene Absorptionsserien beobachtet, die durch die Chlorisotope 35Cl und 37Cl hervorgerufen werden. Damit wird die Bestimmung der Isotopenzusammensetzung möglich.
Bestimmung von Atomabständen und Valenzwinkeln.Da die aus dem R. ablesbare Rotationskonstante B unmittelbar mit dem Trägheitsmoment des Moleküls zusammenhängt (Gl. 1 und 2), lassen sich für zweiatomige Moleküle bei bekannter Masse der Atome Atomabstände mit hoher Genauigkeit direkt berechnen. Für kompliziertere Moleküle genügt die Bestimmung von 3 Trägheitsmomenten zur Berechnung der Atomabstände und Valenzwinkel nicht, sondern es sind zusätzliche Bestimmungsgleichungen erforderlich, die z. B. dadurch erhalten werden können, daß Atome des Moleküls durch Isotope ersetzt werden.
Bestimmung von Dipolmomenten.Bringt man ein rotierendes Dipolmolekül in ein äußeres elektrisches Feld, so kommt es infolge des Stark-Effektes zu einer Aufspaltung der einzelnen Rotationslinien in Stark-Komponenten. Die Größe der Aufspaltung wird als Differenz zwischen der Frequenz mit und ohne äußeres Feld gemessen und hängt von der Stärke des angelegten Feldes und von der Größe des permanenten molekularen Dipolmomentes ab. Bei Kenntnis der äußeren Feldstärke läßt sich aus der Verschiebung das Dipolmoment mit einer Genauigkeit von etwa ±1 % bestimmen.
Kernquadrupolkopplung.Die genaue Analyse der R. hat ergeben, daß bestimmte Moleküle eine Hyperfeinstruktur der Rotationslinien besitzen, die von der Kernquadrupolkopplung (Kernquadrupolresonanz-Spektroskopie) herrühren. Das ist dann der Fall, wenn Atome enthalten sind, die eine Kernspinquantenzahl I > 1/2 und somit ein Kernquadrupolmoment aufweisen, das mit einem inhomogenen elektrischen Feld in Wechselwirkung tritt. Das inhomogene elektrische Feld wird durch eine asymmetrische Ladungsverteilung am Kernort erzeugt und rührt von den Elektronen des Atoms her. Hyperfeinstrukturmessungen können somit zu Aussagen über die Elektronenverteilung in Molekülen benutzt werden.
Bestimmung von Rotationsbarrieren.Durch Wechselwirkung der Rotation von Molekülteilen (z. B. Methylgruppen) und der Rotation des Gesamtmoleküls kann es zu einer Aufspaltung der Rotationslinien in Multipletts kommen, deren Linienabstand von der Höhe der Rotationsbarriere abhängt.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.