Lexikon der Mathematik: Gaußsche Zahlenebene
Deutung und Visualisierung einer komplexen Zahl als zweidimensionaler Vektor.
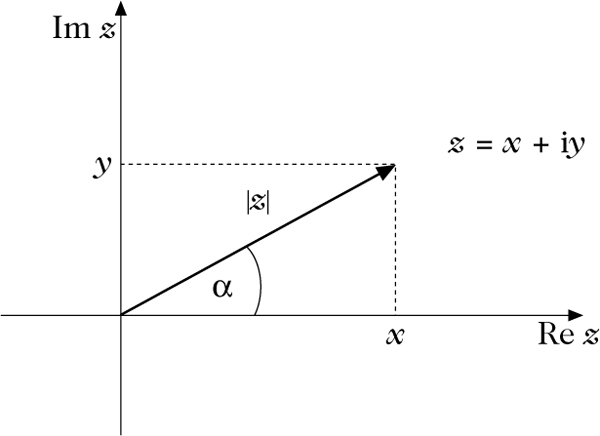
Es sei z = x + iy ∈ ℂ eine komplexe Zahl. Da man komplexe Zahlen nicht als Punkte auf der reellen Achse darstellen kann, braucht man eine über die reelle Achse hinausgehende Darstellungsform, die eine anschauliche Deutung der komplexen Zahl erlaubt. Zu diesem Zweck verwendet man die Gaußsche Zahlenebene. Die Zahl z wird dabei interpretiert als Ortsvektor des Punktes (x, y) in der Ebene.
Komplexe Zahl in der Gaußschen Zahlenebene
Damit kann man die komplexe Addition als Addition von zweidimensionalen Vektoren verstehen. Komplizierter ist die Deutung der Multiplikation, bei der man auf die trigonometrische Darstellung von z zurückgreifen muß. Bezeichnet man mit α den Winkel, den z mit der positiven reellen Achse einschließt, und mit |z| die Länge des z darstellenden Vektors, so folgt aus der geometrischen Darstellung von z sofort die trigonometrische Darstellung
Davon ausgehend kann man die Multiplikation zweier komplexer Zahlen geometrisch so deuten, daß man die reellen Beträge multipliziert und die auftretenden Winkel addiert. Diese Interpretation ist dann auch Grundlage des üblichen Verfahrens zur Radizierung komplexer Zahlen.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.