die im Jahr 1903 durch Teiji Takagi angegebene, durch \begin{eqnarray}f(x)=\displaystyle \sum _{k=1}^{\infty}\frac{\langle {2}^{k}x\rangle}{{2}^{k}}\end{eqnarray}

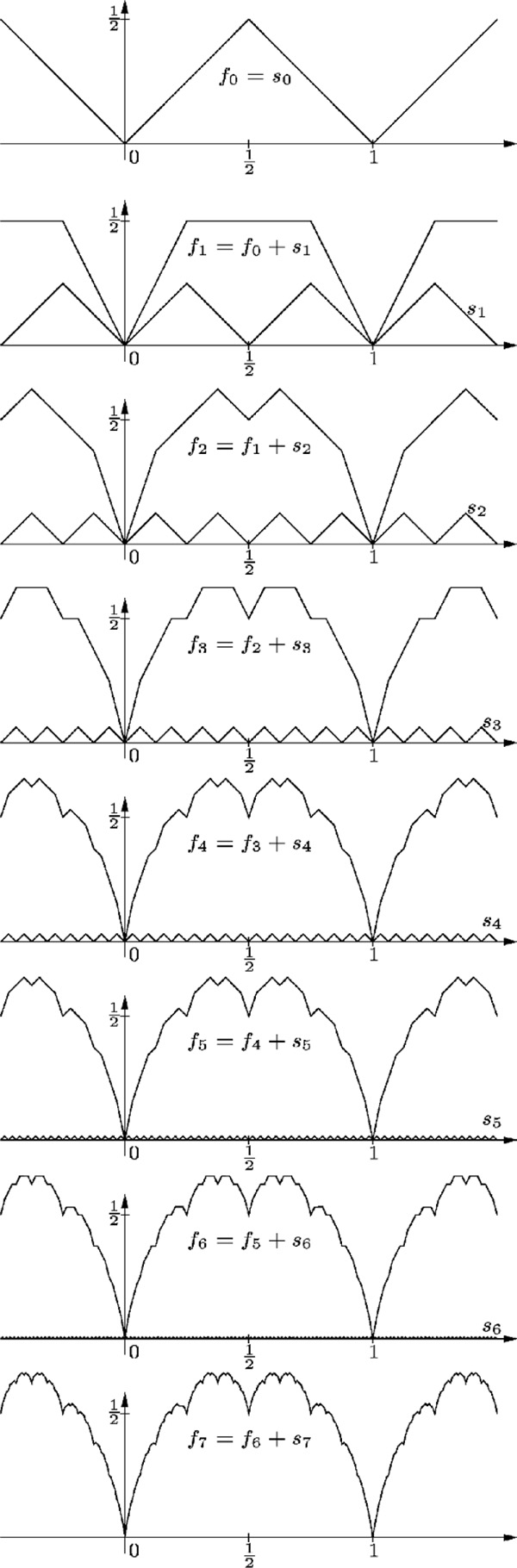
für x ∈ ℝ definierte Funktion f : ℝ → ℝ, wobei ⟨r⟩ den Abstand von r ∈ ℝ zur nächstliegenden ganzen Zahl bezeichnet, also ⟨r⟩ = min{r − ⌊r⌋, ⌈r⌉ − r}. Die Takagi-Funktion ist ein einfaches Beispiel einer nirgends differenzierbaren stetigen Funktion. Die für k ∈ ℕ₀ durch s_k (x) := ⟨2^k x⟩/2^k für x ∈ ℝ definierten Summandenfunktionen s_k : ℝ → ℝ sind Sägezahnkurven, d. h. f ist der punktweise Grenzwert der Summen \({f}_{n}:={\sum}_{k=0}^{n}{s}_{k}\) von Sägezahnfunktionen immer kleinerer Amplitude und Periode.

Wegen 0 ≤ s_n ≤ 1/2ⁿ⁺¹ für alle n ∈ ℕ ist f beschränkt, nämlich 0 ≤ f ≤ 1, und die Konvergenz gleichmäßig. Nach dem Satz von Weierstraß ist f daher stetig. Ferner ist f offensichtlich gerade und 1-periodisch und erfüllt für x ∈ [0, 1] die Funktionalgleichungen \begin{eqnarray}\begin{array}{ccl}f\left(\displaystyle\frac{x}{2}\right) & = & \displaystyle\frac{x+f(x)}{2}\\ f\left(\displaystyle\frac{1+x}{2}\right) & = & \displaystyle\frac{1-x+f(x)}{2},\end{array}\end{eqnarray}

mit deren Hilfe man f (x) für jedes x, das eine endliche dyadische Darstellung hat, ausgehend von f (1) = 0 einfach berechnen kann. Wegen der Stetigkeit von f läßt sich f (x) damit für jedes x beliebig genau annähern. Mittels dyadischer Darstellungen kann man auch zeigen, daß es zu jedem x ∈ ℝ eine gegen x konvergierende Folge (x_n) in ℝ gibt, für die die Folge der Differenzenquotienten (f (x_n) − f (x))/(x_n − x) nicht konvergiert. Folglich ist f nirgends differenzierbar. An Stellen mit endlicher dyadischer Darstellung ist f nicht einmal uneigentlich differenzierbar.

Auf Walter Wunderlich (1954) geht die Beobachtung zurück, daß man aus obigen Funktionalgleichungen zwei affine Abbildungen \begin{eqnarray}\begin{array}{lll}(x,y) & \mapsto & \left(\displaystyle\frac{x}{2},\frac{x+y}{2}\right)\,\,\,\,\,\,\text{und}\\ (x,y) & \mapsto & \left(\displaystyle\frac{1+x}{2},\frac{1-x+y}{2}\right)\end{array}\end{eqnarray}

erhält, die den Graphen von f_{/[0, 1]}auf zwei seiner Teilbögen abbilden, was man heute auch als Selbstähnlichkeit bezeichnet.

Die stückweise linearen Näherungen f_n zur Takagi-Funktion über dem Intervall [0, 1] erhält man auch mit folgendem, als Mittelpunktverschiebung bezeichneten einfachen Verfahren: Ausgehend von der Nullfunktion erhält man durch ‚Verschieben des Funktionswertes‘ an der Stelle \(\frac{1}{2}\) um den Wert \(w:=\frac{1}{2}\) die Funktion f₀. Aus f₀ erhält man durch Verschieben der Funktionswerte an den Stellen \(\frac{1}{4}\) und \(\frac{3}{4}\) um den Wert w² die Funktion f₂ usw.. Geeignete andere Werte für w liefern andere Grenzfunktionen. Beispielsweise führt \(w=\frac{1}{4}\) zu einem Parabe stück (wovon schon Archimedes Gebrauch machte), und \(\frac{1}{2}\lt w\lt 1\) zu einer Kurve der fraktalen Dimension 2 − | log₂w|.

Mit F(x, y) := f (x) + f (y) für x, y ∈ [0, 1] erhält man eine Funktion F : [0, 1] × [0, 1] → ℝ, deren Graph aus naheliegenden Gründen als Takagi-Berg bezeichnet wird (Abb. 2).

F(x, y) := f (x)f (y) liefert ebenfalls eine Funktion, deren Graph einem zerklüfteten Berg ähnelt (Abb. 3).

Auch solche Funktionen lassen sich durch Überlagerung entsprechender, auf ℝ² definierter ℝ-wertiger Sägezahnfunktionen oder durch Mittelpunktverschiebung erhalten. Mittelpunktverschiebung um zufällige Verschiebungswerte w liefert je nach Verteilung der Zufallswerte unterschiedlich ‚rauhe‘ Funktionen, die sich zur rechnerischen Erzeugung von echt erscheinenden Bildern künstlicher Berglandschaften eignen.

[1] Strubecker, K.: Einführung in die höhere Mathematik II. Oldenbourg München, 1967.
[2] Peitgen, H.-O.; Saupe, D.: The Science of Fractal Images. Springer Berlin, 1988.