darstellender Modul für die Bilinearformen.

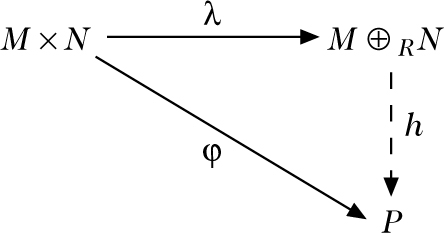
Sei R ein Ring, und seien M und N R–Moduln. Dann ist das Tensorprodukt M ⊗_R N ein R–Modul mit der folgenden universellen Eigenschaft: Es existiert eine bilineare Abbildung λ : M ×N → M ⊗_RN. Wenn φ : M × N → P eine bilineare Abbildung ist, dann existiert ein eindeutig bestimmter Homomorphismus h : M ⊗_RN → P so, daß h ∘ λ = φ ist.

Das Tensorprodukt wird in diesem Fall wie folgt konstruiert. M ⊗_R N ist der Quotient des freien R-Moduls, erzeugt durch {m ⊗ n : m ∈ M, n ∈ N}, nach dem Untermodul erzeugt durch \begin{eqnarray}\begin{array}{l}\{(am+bn)\otimes (cp+dp)-ac\cdot m\otimes p\\\quad -ad\cdot m\otimes q-bc\cdot n\otimes p-bd\cdot n\otimes q\\\qquad :a,b,c,d\in R,m,n\in M,p,q\in N\}.\end{array}\end{eqnarray}

Wenn S eine R–Algebra ist, dann ist M ⊗_R S ein S– Modul mit der Multiplikation s · m ⊗ s′ = m ⊗ ss′. Eine wichtige Eigenschaft des Tensorprodukts ist die Beziehung zum Funktor Hom: Die kanonische Abbildung \begin{eqnarray}\phi :{\text{Hom}}_{R}(M{\otimes}_{R}N,P)\to {\text{Hom}}_{R}(M,{\text{Hom}}_{R}(N,P)),\end{eqnarray}

definiert durch ϕ(λ)(m)(n) = λ(m ⊗ n), ist ein Isomorphismus.