»Haben Sie sich schon einmal gefragt, ob es neben der ersten, zweiten und anderen ganzzahligen Ableitungen auch so etwas wie eine eineinhalbfache Ableitung gibt?« Mit dieser Frage verblüffte mich ein Physikprofessor in meinem ersten Semester an der Universität. Nein, ich hatte bis zu diesem Zeitpunkt tatsächlich noch nie darüber nachgedacht, ob es »fraktionale Ableitungen« gibt. Wie steht es mit Ihnen?

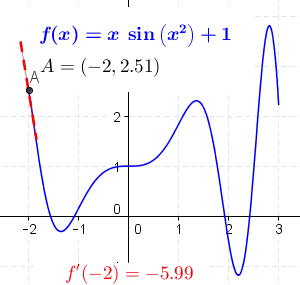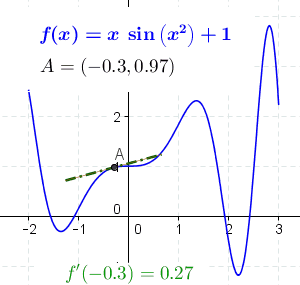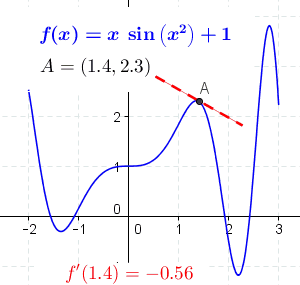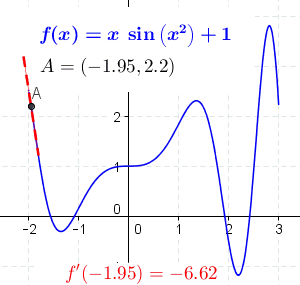
In der Schule lernt man Ableitungen zunächst geometrisch kennen: Dafür pickt man sich einen Punkt auf einer Kurve heraus und zoomt so lange in die Umgebung des Punktes hinein, bis der Kurvenausschnitt einer Gerade ähnelt. Die Steigung dieser Geraden entspricht der Ableitung der Kurve an diesem Punkt. Die Ableitung gibt also an, wie sich die Richtung der Kurve ändert. Und das lässt sich auch abseits der Geometrie verallgemeinern: Die Ableitung einer Funktion entspricht ihrer Änderungsrate – so ist die Beschleunigung nichts anderes als die Ableitung der Geschwindigkeit.

Wenn man sich diese Bedeutung vor Augen führt, erscheint es nicht sinnvoll, über eine »halbe Ableitung« nachzudenken. Doch wie sich herausstellt, lassen sich durch diese Art der fraktionalen Analysis komplizierte Vorgänge modellieren, etwa die Ausbreitung eines Wirkstoffs im menschlichen Körper oder der Alterungsprozess einer Batterie.

Die Geschichte der Analysis ist von einem tief greifenden Konflikt geprägt: Im 17. Jahrhundert entwickelten sowohl Isaac Newton als auch Gottfried Wilhelm Leibniz unabhängig voneinander die Grundlagen der heutigen Analysis – woraus sich unschöne Plagiatsvorwürfe ergaben. Inzwischen ist dieser Zweig der Mathematik aus unserem Leben nicht mehr wegzudenken. Selbst in der Schule sucht sie uns heim: Die Infinitesimalrechnung begegnet so gut wie allen Schülerinnen und Schülern in Form der Kurvendiskussion.

Mit Ableitungen und Integralen lassen sich aber nicht nur geometrische Objekte besser verstehen – ohne sie könnten wir unsere Welt unmöglich beschreiben. Denn alles, was in unserem Universum geschieht, besitzt eine gewisse Dynamik: Die Zeit vergeht, Dinge verändern sich. Um solche Änderungen zu beschreiben, sind Ableitungen unerlässlich. Es überrascht also nicht, dass die fundamentalen Gleichungen der Physik – die der allgemeinen Relativitätstheorie und die des Standardmodells der Teilchenphysik – Ableitungen enthalten. Und die sind natürlich ganzzahlig.

Diese Gleichungen können zwar rein theoretisch unsere Welt beschreiben, doch sie sind so kompliziert, dass man sie außer für Spezialfälle nie exakt lösen kann. Möchte man alltagsnähere Phänomene beschreiben, nutzt man daher andere Ansätze. Um zum Beispiel das Fließen einer Flüssigkeit zu beschreiben, greift man auf die so genannten Navier-Stokes-Gleichungen zurück, die mehrere einfache Ableitungen enthalten. Zwar sind auch diese meist nicht lösbar, lassen sich aber recht gut am Computer simulieren. Elastische Festkörper wie eine Feder enthalten hingegen zweifache Ableitungen, da ihre Bewegung wie bei einer gespannten Feder beschleunigt wird.

Ganzzahlige Ableitungen eignen sich nicht immer für Polymere

Es gibt aber auch Substanzen wie amorphe Polymere, die viskoelastisch sind: Diese sind besonders schwer durch mathematische Gleichungen zu erfassen, denn sie befinden sich an der Grenze zwischen Festkörper (zweifache Ableitung) und Flüssigkeit (einfache Ableitung). Das macht es schwierig, solche Systeme am Computer zu simulieren und damit ihr Verhalten vorherzusagen. Wie sich herausstellt, sind fraktionale Ableitungen in solchen Fällen hilfreich, denn sie können Grenzfälle besser erfassen. Zum Beispiel könnte man versuchen, die Polymere durch Gleichungen zu beschreiben, in der eine eineinhalbfache Ableitung vorkommt. Einen ähnlichen Ansatz haben die Forscher um Andrea Genovese von der Universität Neapel im Oktober 2022 verwendet, um die Temperaturabhängigkeit von amorphen Polymeren zu untersuchen.

Es gibt sogar Ansätze, die Gleichungen der allgemeinen Relativitätstheorie abzuändern und fraktionale Ableitungen einzuführen. Ein solches Modell haben die Physiker um Miguel García-Aspeitia von der Universidad Iberoamericana Ciudad de México im Jahr 2022 beschrieben. Demnach befolgten die Materieteilchen im frühen Universum, die sich wie Fluide verhielten, Bewegungsgleichungen mit fraktionalen Ableitungen. Damit hoffen die Physiker, ein kosmologisches Modell zu entwickeln, das ohne Dunkle Energie auskommt.

Neben dieser etwas ausgefallenen Anwendung hat sich die fraktionale Analysis in vielen Bereichen als nützlich erweisen, etwa bei der Beschreibung von Wärmeleitung in Materialien, Diffusion in porösen Medien, Ölströmungen in Pipelines, Ausbreitungsdynamiken von Covid-19 und vielem mehr. Ein Vorteil der Methode besteht darin, dass es durch die kompakte Beschreibung weniger Parameter gibt, die man für all diese komplexen Prozesse simulieren muss. Dadurch nimmt die Rechendauer ab und man erhält genauere Ergebnisse.

Fraktionale Ableitungen haben ein Gedächtnis

Doch der wahrscheinlich bedeutendste Vorteil besteht darin, dass fraktionale Ableitungen eine Art Gedächtnis besitzen: In den abgeleiteten Funktionen sind Details der vergangenen Zustände codiert. Wenn man also eine fraktionale Ableitung in der Zeit bildet, dann berücksichtigt man automatisch, wie sich das System zu vergangenen Zeitpunkten verhalten hat. Das ist unter anderem bei der Untersuchung von Batterien nützlich, deren Kapazität vom bisherigen Ladeverhalten abhängt: Wie oft wurde die Batterie schon aufgeladen? Hat man immer gewartet, bis sie leer ist, oder wurde sie zu einem beliebigen Zeitpunkt an die Steckdose gehängt?

Um die Vorteile der fraktionalen Ableitungen voll erfassen zu können, muss man einen Blick hinter die Kulissen wagen und den mathematischen Details ins Gesicht sehen. Aber keine Angst, sie unterscheiden sich im Prinzip kaum von dem, was uns bereits in der Schule begegnet.

Die zögerlichen Anfänge der fraktionalen Analysis

Als der französische Mathematiker Guillaume de l'Hôpital die Arbeiten zur Infinitesimalrechnung von Leibniz durchsah, hatte er wohl keine Kurven oder konkrete Anwendungen vor Augen. Stattdessen fasste er die Ableitung ^d⁄_dx als abstrakten mathematischen Operator auf, der eine Funktion f(x) auf eine andere Funktion f'(x) abbildet. So wird durch die Ableitung zum Beispiel aus einer Parabel f(x) = x² eine Gerade: f'(x) = 2x. Ebenso kann man auch eine zweifache Ableitung (^d⁄_dx)² finden, eine dritte und so weiter. De l'Hôpital fragte Leibniz daher im Jahr 1695 in einem Brief, was herauskäme, wenn man eine halbe Ableitung bilden würde, also (^d⁄_dx)^1/2. Leibniz antwortete: »Es wird zu einem Paradoxon führen, aus dem eines Tages nützliche Konsequenzen gezogen werden.«

Auch wenn bisher kein Paradoxon gefunden wurde, lag Leibniz mit dem zweiten Teil seiner Aussage erstaunlich richtig. Doch es sollte noch bis zum frühen 19. Jahrhundert dauern, bis Mathematiker herausfanden, wie man eine fraktionale Ableitung definieren sollte. Den Schlüssel lieferte schließlich die umgekehrte Operation: das Integral.

Denn 1823 hatte der französische Mathematiker Augustin-Louis Cauchy eine nützliche Formel für mehrere hintereinander ausgeführte Integrationen entwickelt. Anstatt mühsam viele Male nacheinander eine Funktion zu integrieren, kann man gemäß der Cauchy-Formel auch nur ein einziges Integral auswerten. Im Detail sieht die dazugehörige Gleichung so aus:

\[ \begin{split} I^n f(x) &= \int_a^x\int_a^{y_1} \int_a^{y_2}... \int_a^{y_{n-1}} f(y_n) dy_n dy_{n-1}... dy_y\\ &= \frac{1}{(n-1)!} \int_a^x (x-y)^{n-1}f(y) \ dy \end{split}\]

Hierbei ist a eine beliebige Konstante, die später noch eine große Rolle spielen wird: nämlich die des Gedächtnisses. Diese Gleichung ermöglicht es, den Integralbegriff zu verallgemeinern. Denn theoretisch könnte man für n auch eine Bruchzahl oder gar eine irrationale Zahl einsetzen. Das führt zunächst nur an einer Stelle zu Problemen: bei dem Faktor 1/(n−1)!

Dank eines Integrals zur fraktionalen Ableitung

Denn das !-Symbol steht nicht für ein Ausrufezeichen, sondern eine mathematische Operation, die Fakultät. Dabei handelt es sich um ein Produkt von absteigenden Zahlen, zum Beispiel: 5! = 5·4·3·2·1. Die Fakultät ist somit nur für natürliche Zahlen definiert. Doch glücklicherweise gibt es auch eine Verallgemeinerung des Konzepts, die so genannte Gamma-Funktion Γ, die der Schweizer Mathematiker Daniel Bernoulli im 18. Jahrhundert eingeführt hat: Sie definiert eine Art Fakultät für alle reellen Zahlen, wobei Γ(n) = (n−1)!, falls n eine natürliche Zahl ist.

Damit stand dem fraktionalen Integrieren nichts mehr im Weg! Und tatsächlich kann n nun beliebige reelle Werte annehmen, also auch π oder √2. Doch wir fangen lieber mit einem einfachen Beispiel an und berechnen die halbe Integration von f(x) = x:

\[ I^\frac{1}{2} f(x) =\frac{1}{\Gamma\left(\frac{1}{2}\right)} \int_a^x \frac{y}{\sqrt{x-y}}\ dy = \frac{2}{3\sqrt{\pi}}\sqrt{x-a}(2x+a) \]

Diese Erkenntnis hatten Bernhard Riemann und Joseph Liouville Mitte des 19. Jahrhunderts, weshalb diese Form des fraktionalen Integrals ihren Namen trägt. Die beiden Mathematiker erkannten auch, dass es möglich ist, das Ergebnis ganz normal abzuleiten. Auf diese Weise lassen sich fraktionale Ableitungen bilden: Man integriert erst um einen Wert, der nicht ganzzahlig ist, und leitet dann auf herkömmliche Weise ab. Indem man also das vorige Beispiel ableitet, erhält man die halbe Ableitung von f(x) = x:

\[ \frac{d}{dx} I^\frac{1}{2} f(x) = \frac{2x-a}{\sqrt{\pi(x-a)}} \]

Für den Fall, dass a = 0 ist, nimmt die halbe Ableitung von x also die Form √(4/π)·√x an. Der Graph der Wurzelfunktion verläuft auch tatsächlich zwischen f(x) = x und dessen erster Ableitung f'(x) = 1. So erhält die fraktionale Ableitung auch einen geometrischen Sinn: Sie führt Funktionen zwischen den ganzzahligen Ableitungen ineinander über.

Damit hatten Liouville und Riemann den Grundstein der fraktionalen Analysis gelegt. Doch in den ersten Jahrzehnten war das nur manchen Mathematikerinnen und Mathematikern ein Begriff. Fraktionale Ableitungen schienen eine nette Spielerei, allerdings ohne ernsthafte Anwendung. Tatsächlich gab es bis zum Jahr 1974 nur ein einziges Buch und einen Tagungsband zu dem Thema. Doch dann begannen auch Fachleute anderer Bereiche das Potenzial der ungewöhnlichen Ableitungen zu erkennen. Inzwischen gibt es jährlich zahlreiche Veröffentlichungen mit viel versprechenden Ergebnissen. Dabei spielt vor allem der Faktor a, der vom Integrieren übrig bleibt, eine wichtige Rolle.

Beim fraktionalen Ableiten ist man gezwungen, ein ganzes Intervall zu berücksichtigen (etwa von a bis zur eigentlichen Variablen x), deshalb wird eine Funktion nicht bloß punktweise ausgewertet. Damit enthält die fraktionale Ableitung wesentlich mehr Informationen als eine gewöhnliche Ableitung. Das hat entscheidende Vorteile, vor allem wenn man Systeme simulieren möchte, deren Eigenschaften stark von vergangenen Zuständen abhängen. Zwar lassen sich solche Systeme auch mit gewöhnlichen Ableitungen beschreiben, doch die Gleichungen fallen wesentlich komplizierter aus.

Mit fraktionalen Ableitungen zu einem besseren Covid-19-Modell

Ein Beispiel dafür ist ein Modell, das die Ausbreitung von Covid-19 beschreiben soll. Die gewöhnliche Version, die bloß ganzzahlige Ableitungen enthält, stützt sich auf sechs komplizierte Gleichungen, die miteinander gekoppelt sind. Solche Gleichungssysteme zu lösen ist nicht nur aufwändig, sie führen auch häufig zu Ungenauigkeiten. Daher haben der Mathematiker Zeeshan Ali und seine Kollegen von der Monash University in Australien einen fraktionalen Ansatz gewählt, um die Covid-19-Ausbreitung zu simulieren. Dieser besteht aus einer einzigen Gleichung – und konnte die Beobachtungsdaten besser wiedergeben.

Trotz all dieser Fortschritte und einer etwa 300-jährigen Geschichte beginnt die Fachwelt gerade erst, das Gebiet der fraktionalen Analysis wahrzunehmen. So sind die physikalischen und geometrischen Bedeutungen der fraktionalen Ableitungen noch immer nicht vollständig geklärt. Das liegt vielleicht daran, dass viele Personen – selbst solche mit wissenschaftlichem Bezug – noch nie davon gehört haben. Bleibt zu hoffen, dass sich das in Zukunft ändert, denn wer weiß, was das Gebiet noch alles zu bieten hat.