manchmal auch R-Algebra oder nur Algebra genannt, ist ein Modul A über dem kommutativen Ring R, der neben der Modulstruktur noch eine zusätzlich Multiplikation · besitzt, so daß

1. A ein (nicht notwendig assoziativer) Ring ist und
2. die Verträglichkeitsbedingungen

gelten.

Besitzt die Algebra ein neutrales Element e der Multiplikation, so ist e eindeutig und heißt Einselement der Algebra. Die Algebra A nennt man dann Algebra mit Eins. Eine Algebra A heißt kommutativ, falls gilt ∀a, b ∈ A : a · b = b · a.

Eine Algebra heißt assoziativ, falls die Multiplikation assoziativ ist, d. h. \begin{eqnarray}\forall a,b,c\in A:(a\cdot b)\cdot c=a\cdot (b\cdot c).\end{eqnarray}

Manchmal versteht man unter einer Algebra immer eine assoziative Algebra und benennt die restlichen explizit als nichtassoziative Algebren. Wichtige Beispiele für assoziative Algebren sind die Polynomringe und für nichtassoziative Algebren die Lie-Algebren. Ist der zugrundeliegende Ring ein Körper 𝕂, so ist A ein Vektorraum über 𝕂 und A heißt Algebra über 𝕂, bzw. 𝕂-Algebra, bzw. wenn der Körper feststeht auch nur Algebra.

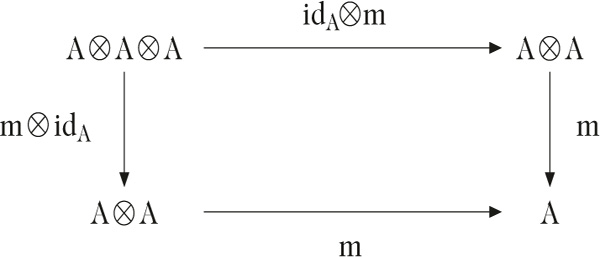
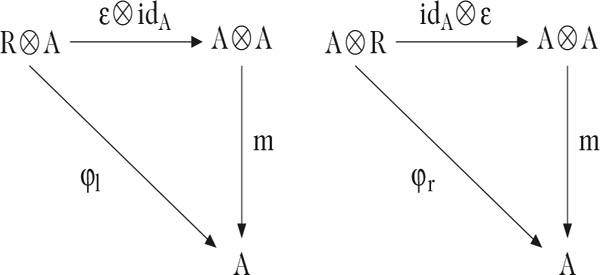
Im Zusammenhang mit allgemeineren Konzepten ist die folgende äquivalente Beschreibung einer assoziativen Algebra A mit Einselement 1_A über einem kommutativen und assoziativen Ring R mit Einslement 1_R nützlich. Die äquivalente Beschreibung besteht aus einem Tripel (A, m, ϵ) mit einem R-Modul A und den R-linearen Abbildungen m : A ⊗ A → A (Multiplikation) und ϵ : R → A (Einheit), die den folgenden Bedingungen genügen:

1. Es gilt m ∘ (m ⊗ id_A) = m ∘ (id_A ⊗ m) für die Abbildungen A ⊗ A ⊗ A → A.

   

2. m ∘ (ϵ ⊗ id_A) = φ_l und m ∘ (id_A ⊗ ϵ) = φ_r, mit φ_l : R ⊗ A → A, α ⊗ x → αx und φ_r : A ⊗ R → A, x ⊗ α → αx.

   

Die Beziehung zur ersten Beschreibung wird durch \begin{eqnarray}m(a\otimes b)=a\cdot b & \text{und} & \varepsilon (\alpha )=\alpha \cdot {1}_{A}\end{eqnarray}

hergestellt.