Lexikon der Mathematik: Denjoy-Young-Saks, Satz von
besagt, daß für jede auf einem offenen Intervall I ⊂ ℝ definierte
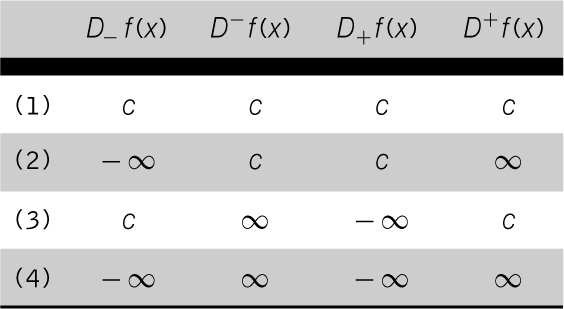
Funktion f : I → ℝ für fast alle x ∈ I (also mit Ausnahme höchstens einer Nullmenge) die DiniAbleitungen von f an der Stelle x einen der folgenden vier Fälle mit einem von x abhängigen c ∈ ℝ erfüllen.
© Springer-Verlag GmbH Deutschland 2017 Bild vergrößern
Im Fall (1) ist f differenzierbar in x mit f′(x) = c.
Copyright Springer Verlag GmbH Deutschland 2017
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.