Lexikon der Mathematik: Koalgebra
(über einem Ring R), ein Tripel (C, Δ α) bestehend aus einem Modul C über dem kommutativen Ring R mit 1, einer R-linearen Abbildung Δ : C → C⊗C, die Komultiplikation oder Diagonalabbildung genannt wird, und einer R-linearen Abbildung α : C → R, die Koeinheit oder Augmentation genannt wird.
Es seien die folgenden Bedingungen erfüllt:
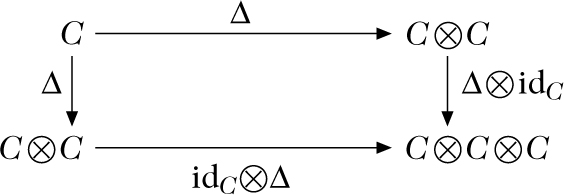
- (Δ⊗idC)○Δ = (idC⊗Δ)○Δ für die Abbildungen C → C ⊗ C ⊗ C.
- (α ⊗ idC) ○ Δ = tl und (idC ⊗ α) ○ Δ = tr mit den Abbildungen tl : C → R ⊗ C, x ↦ 1 ⊗ x und tr : C → C ⊗ R, x ↦ x ⊗ 1.
Ein Beispiel einer Koalgebra ist die Gruppenalgebra 𝕂[G] einer Gruppe G über einem Körper 𝕂. Sie ist der Vektorraum über 𝕂 mit Basis {eg | g ∈ G} und Multiplikation m, definiert durch
Die Komultiplikation
In der Tat ist 𝕂[G] eine Bialgebra.
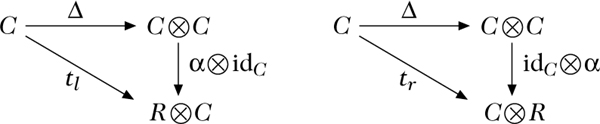
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.