Lexikon der Mathematik: zweidimensionale Wavelets
die Funktionen, die das orthogonale Komplement W0 von V0 in V1 aufspannen, wobei V0 der Grundraum einer zweidimensionalen Multiskalenanalyse ist (zweidimensionale Wavelet-Basis).
Ein einfacher Weg, eine orthonormale Basis für L2(ℝ2) zu konstruieren, ist, mit einer orthonorma-len Basis des L2(ℝ) zu beginnen und dann Tensorprodukte der eindimensionalen Funktionen zu betrachten. Man startet mit einem orthogonalen eindimensionalen Wavelet ψ und einer orthogonalen eindimensionalen Skalierungsfunktion φ. Dann betrachtet man das Tensorprodukt φ(x)φ(y) in V0 und erzeugt mit der Dilatationsmatrix
Man kann zweidimensionale Wavelets auch direkt mit Hilfe eines zweidimensionalen Generators, zum Beispiel eines Box-Splines, erzeugen.
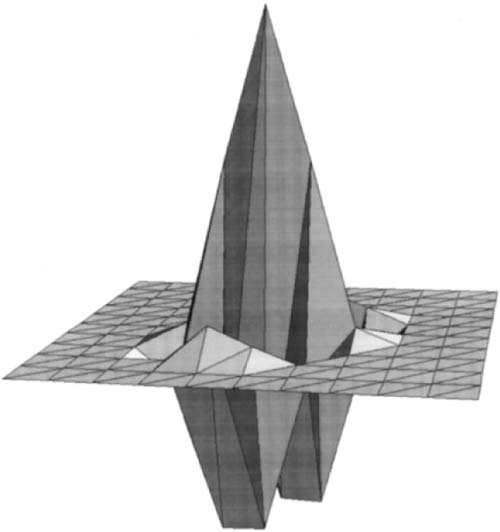
Zweidimensionales Wavelet
Eine weitere Möglichkeit ist es, von der Diagonalmatrix A verschiedene Dilatationsmatrizen zu verwenden. Beispielsweise ist die Rotationsmatrix
eine geeignete Wahl für eine Skalierungsmatrix. Die Verallgemeinerung der Haar-Funktion führt in diesem Fall auf die Indikatorfunktion einer frak-talen Menge, den sogenannten twin dragon. Wegen | det(M)| = 2 ist hier nur ein Wavelet (1 = | det(M)| − 1) nötig, um den Komplementraum zu erzeugen.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.