Lexikon der Mathematik: Das Erlanger Programm von Felix Klein
Mit dem Erlanger Programm von 1872 [7] formulierte Felix Klein seine Idee, mit Hilfe von Transformationsgruppen verschiedene Geometrien voneinander zu unterscheiden.
Für jede Geometrie gibt es eine Hauptgruppe, unter welcher deren Lehrsätze richtig bleiben, und eine spezielle Untergruppe, welche ihre Begriffe ungeändert läßt.
Da beispielsweise die Sätze Euklids gültig bleiben, wenn irgendeine Bewegung, Spiegelung oder Dilatation durchgeführt wird, besteht die Hauptgruppe der euklidischen Geometrie aus der Gruppe der Ähnlichkeiten, die durch Spiegelungen und Dilatationen erzeugt wird. Dilatationen können Längen oder Abstände ändern, wohingegen sämtliche Bewegungen durch Kompositionen von Spiegelungen erhalten werden können; deshalb besteht die spezielle Untergruppe aus der Gruppe der Isometrien, welche durch Spiegelungen erzeugt wird.
Da es in den nichteuklidischen Geometrien keine Entsprechung für die Ähnlichkeit gibt, fallen in einem solchen Fall die Hauptgruppe und die spezielle Untergruppe zusammen. Die sphärischen und hyperbolischen Geometrien unterscheiden sich von elliptischen Geometrien durch topologische Betrachtungen: Die elliptische Ebene (die aus einer Kugel durch Gleichsetzung von Gegenpunkten entsteht) ist nicht orientierbar, ebenso wie der elliptische Raum.
Die projektive Geometrie [2, Kapitel 14; 9] handelt von Punkten, Geraden und Ebenen, deren einzige Beziehung die der Inzidenz ist. Ihre Abstände und Winkel werden nicht gemessen und ihre Sätze bleiben richtig, wenn sie dualisiert werden. Ihre Hauptgruppe ist deshalb die Gruppe der Kollineationen und Korrelationen, von denen beide projektiv und antiprojektiv sind. Die spezielle Untergruppe, die von den Projektivitäten erzeugt wird, ist die Gruppe der projektiven Kollineationen.
Indem man eine Gerade der projektiven Ebene (oder eine Ebene des projektiven Raumes) auszeichnet, leitet man die affine Geometrie her. Ihr geht es um Parallelität und Flächen (und Volumen), Winkel werden jedoch nicht gemessen. Die Hauptgruppe ist die Gruppe der Affinitäten [3], die spezielle Untergruppe ist die Gruppe der Äquiaffinitäten.
Die inversive Geometrie, welche Klein „Die Geometrie der reciproken Radien“ nannte, handelt von Punkten und Kreisen (oder Kugeln). Ihre Hauptuntergruppe wird durch Inversionen erzeugt. Orthogonalität kann man mit dem Begriff der Berührung definieren, und aufgrund der Stetigkeit können Winkel gemessen werden. Anstelle des bekannten Abstands zwischen Punktepaaren gibt es den inversiven Abstand zwischen Paaren von Kreisen (oder Kugeln).
Ein Vergleich mit der euklidischen Geometrie zeigt, daß wir nur einen Punkt im Unendlichen unterscheiden können; die Kreise, die durch diesen Punkt gehen, werden mit den euklidischen Geraden gleichgesetzt. Zwei beliebige disjunkte Kreise können in konzentrische Kreise invertiert werden, und der inversive Abstand zwischen zwei disjunkten Kreisen kann durch log(a/b) beschrieben werden, wobei a und b (mit a >b) die Radien von zwei beliebigen konzentrischen Kreisen sind, in welche die beiden disjunkten Kreise invertiert werden können.
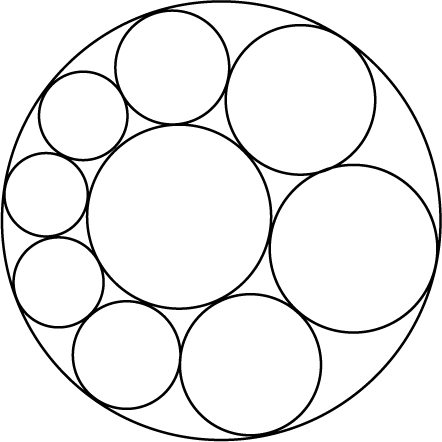
Bild 1
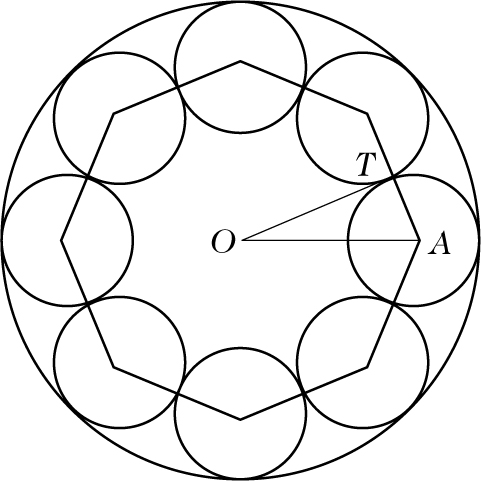
Bild 2
Ein gutes Beispiel für die Nützlichkeit des Erlanger Programms liefert der Schließungssatz von Steiner [2]. Angenommen, wir haben zwei (sich nicht schneidende) Kreise, deren einer im Inneren des anderen liegt, und einen Ring von Kreisen, die sowohl einander der Reihe nach als auch die beiden <?PageNum _72Ursprungskreise berühren (siehe Bild 1). Es kann dann vorkommen, daß der letzte Kreis den ersten berührt, so daß sich der Ring schließt. Wenn dies einmal auftritt, tritt dies immer auf, wie auch die Lage des ersten Kreises im Ring sein mag.
Da dieses Theorem nur Kreise und ihre Tangenteneigenschaften betrifft (zwei Kreise berühren sich, wenn sie nur einen gemeinsamen Punkt haben), ist es Teil der inversiven Geometrie. Man kann den Satz beweisen, indem man die beiden ursprünglichen Kreise in konzentrische invertiert, für welche die Behauptung offensichtlich gilt, wie in Bild 2 dargestellt.
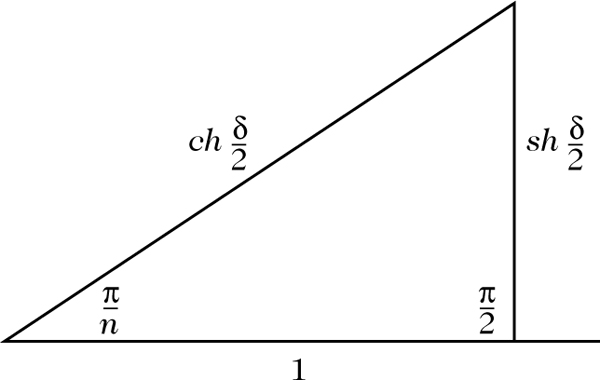
Bild 3
Genauer ausgedrückt: Besteht der Ring aus n Kreisen, müssen die beiden Grundkreise einen bestimmten inversiven Abstand δ, welcher eine Funktion von n [5, S. 127] ist, voneinander haben. Tatsächlich gilt wie in Bild 3:
Es kann vorkommen, daß zwei verschiedene Geometrien isomorphe Gruppen besitzen. Der offensichtlichste Fall liegt bei der inversiven Ebene und dem hyperbolischen dreidimensionalen Raum [1] vor. Die Gruppe der Homographien und Antihomographien, die durch Inversionen in die ∞3 Kreise der Ebene erzeugt werden, ist isomorph zu der Gruppe der hyperbolischen Isometrien, die ihrerseits durch Spiegelungen in die ∞3 Ebenen des hyperbolischen Raumes erzeugt werden. Dieser Isomorphismus läßt sich übersichtlich in einer Art „Wörterbuch“ [8, S. 60-89; 4, S. 266] darstellen:
Als eine Transformation komplexer Zahlen [8, S. 85] entspricht die loxodromische Homographie
Die bemerkenswerte Leistungsfähigkeit des Erlanger Programms zeigt sich in seiner Anwendbarkeit auf Situationen, die Klein selbst sich noch nicht vorzustellen vermochte. So sind die verschiedenen endlichen Geometrien mit einer wichtigen Familie von Gruppen [6, S. 93] verbunden.
Genauer ausgedrückt: Klein schien sich im Jahr 1872 noch nicht darüber bewußt gewesen zu sein, daß von Staudt 1857 [10, S. 87–88] geäußert hatte, es gebe (q2 + q + 1) Punkte in der projektiven Ebene und (q3 + q2 + q + 1) Punkte im dreidimensionalen Raum, vorausgesetzt, es liegen (q + 1) Punkte auf einer Geraden. Obwohl von Staudt die Möglichkeit einer endlichen Geometrie in Erwägung zog und damit die Ergebnisse von G. Fano vorwegnahm, hatte er nicht die leiseste Ahnung einer Beziehung zur Gruppentheorie: Er sollte niemals erfahren, daß q eine Potenz einer Primzahl sein sollte!
(Übersetzung: Brigitte Post)
Literatur
[1] Coxeter, H.S.M.: The inversive plane and hyperbolic space. Abh. Math. Sem. Univ. Hamburg 29, 1966.
[2] Coxeter, H.S.M.: Unvergängliche Geometrie (2. Auflage). Birkhäuser, Basel, 1981.
[3] Coxeter, H.M.S.: Affine regularity. Abh. Math. Sem. Univ. Hamburg 62, 1992.
[4] <?PageNum _73Coxeter, H.M.S.: Non-Euclidean Geometry (6. Auflage). Mathematical Association of America, Washington, DC, 1998.
[5] Coxeter, H.M.S., Greitzer S.L.: Geometry Revisted. Mathematical Association of America, Washington, DC, 1967.
[6] Coxeter, H.M.S., Moser W.O.J.: Generators and Relations for Discrete Groups (4. Auflage). Springer-Verlag, Berlin, 1980.
[7] Klein, F.: The Erlanger Program. The Math. Intelligencer 0, 1977.
[8] Schwerdtfeger, Hans: The Geometry of Complex Numbers. University of Toronto Press, 1962.
[9] Staudt von, G.K.C.: Geometrie der Lage. Nürnberg, 1847.
[10] Staudt von, G.K.C.: Beiträge zur Geometrie der Lage. Nürnberg, 1856.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.