Lexikon der Mathematik: F-Test
ein spezieller Signifikanztest zum Prüfen der Gleichheit der Varianzen zweier unabhängiger normalverteilter Zufallsgrößen X und Y.
Seien X normalverteilt mit dem Erwartungswert μX und der Varianz \(\sigma_{X}^{2}\) und Y normalverteilt mit dem Erwartungswert μY und der Varianz \(\sigma_{Y}^{2}\). Die zu prüfenden Hypothesen lauten im zweiseitigen Testfall
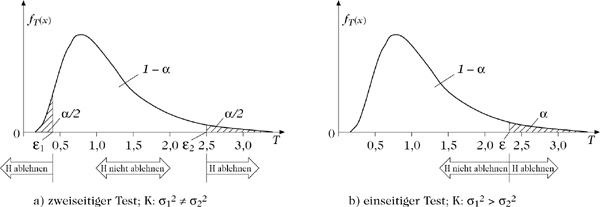
Verteilungsdichte von T (n1 = 21, n2 = 16);Ablehne- und Annahmebereich von H für α = 0,05
Ein Beispiel: Zwei Gruppen von Studenten mit n1 = 15 und n2 = 13 Teilnehmern werden nach zwei unterschiedlichen Lehrmethoden ausgebildet. In einem abschließenden Test erreichten beide Gruppen eine durchschnittliche Punktzahl von \(\bar{x}=\bar{y}=50,7\) Punkten bei einer Standardabweichung von s1 = 4,3 Punkten in der 1. Gruppe und s2 = 9,1 Punkten in der 2. Gruppe. Es soll nun auf einem Signifikanzniveau von α = 0,02 geprüft werden, ob der beobachtete Unterschied in den Standardabweichungen signifikant ist. Es ist der zweiseitige Test durchzuführen. Für die Testgröße T erhalten wir
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.