Lexikon der Mathematik: hyperbolische Tangensfunktion
Tangens hyperbolicus, eine der Hyperbelfunktionen, nämlich die durch
Es gilt
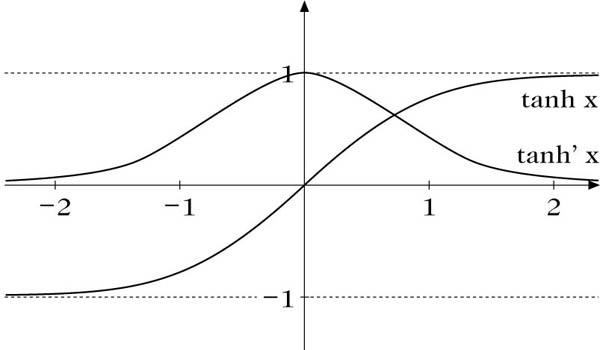
Hyperbolische Tangensfunktion
Für
Setzt man die Hyperbelfunktionen und die trigonometrischen Funktionen in die komplexe Ebene fort, so gilt tanh iz = i tan z für z ∈ ℂ. Insbesondere ist
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.