ein Assoziationsmaß bzw. Rangkorrelationskoeffizient.

Er wird wie der Spearmansche Korrelationskoeffizient auf der Basis der Rangzahlen (geordnete Stichprobe) r(x_i)und r(y_i) einer Stichprobe (x_i,y_i), i = 1,…,n zweier Zufallsvariablen (X, Y) berechnet. Man ordnet dazu die Beobachtungspaare (x_i, y_i), i = 1,…,n nach aufsteigenden Rangzahlen r(x_i) der ersten Komponente x_i. Dadurch wird auch eine Reihenfolge der Rangzahlen r(y_i) festgelegt. In dieser Reihenfolge wird für jede Rangzahl r(y_i) die Anzahl q_i der Rangzahlen r(y_j)ermittelt, die kleiner oder gleich r(y_i) sind und in der Reihenfolge hinter r(y_i) stehen. Das Kendall-sche τ ergibt sich dann zu \begin{eqnarray}\tau =1-\frac{4\displaystyle {\sum }_{i=1}^{n}qi}{n(n-1)}.\end{eqnarray}

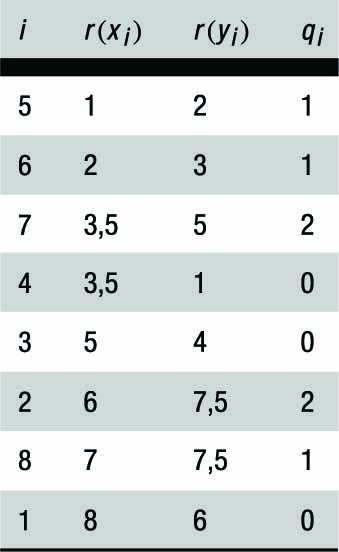
Ein Beispiel. Zwei Personen stellen eine Bewertungstabelle für 8 zufällig ausgewählte Gemälde auf. Sie dürfen 1 bis 8 Punkte und auch, wenn ihnen mehrere Gemälde gleich gut gefallen, mittlere Punkte vergeben. Die Punkteskala gibt gibt natürlich nur die Rangfolge an, so daß wir zur Schätzung der Korrelation zwischen den ‘Geschmäckern’ der Personen A und B nur einen Rangkorrelationskoeffizienten berechnen können. Die Punktzahlen sind in folgender Tabelle gegeben. Für den τ-Koeffizient ergibt sich dann: \begin{eqnarray}\begin{array}{ccc}\tau & = & 1-\frac{4\displaystyle {\sum }_{i=1}^{n}q_{i}}{n(n-1)}\\ & = & 1-\frac{4(1+1+2+2+1)}{8.7}\\ & = & 1-\frac{4.7}{8.7}=0,5.\end{array}\end{eqnarray}