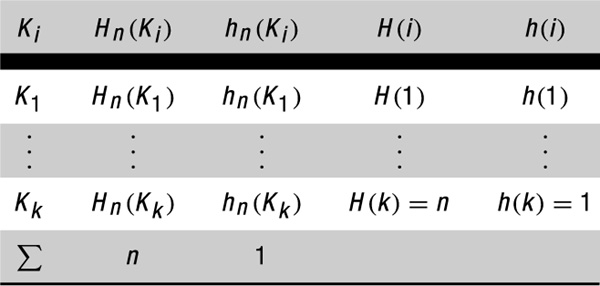
Die Klasseneinteilung ist eine Methode zur Ermittlung von Hypothesen über die Gestalt der Dichtefunktion bzw. zur Verdichtung und Auswertung von Stichprobendaten einer stetigen Zufallsgröße. Sei X eine stetige Zufallsgröße mit dem Wertebereich \({\mathcal{X}}\) und (x₁, …, x_n) eine konkrete Stichprobe von X. Um eine Vorstellung über die Gestalt der Verteilung von X in der zugrundeliegenden Grundgesamtheit zu bekommen, wird der Wertebereich \({\mathfrak{X}}\) von X in k disjunkte Intervalle \({K}_{1},\ldots,{K}_{k},{K}_{i}=({a}_{i}^{u},{a}_{i}^{0}]\), die auch Klassen genannt werden, zerlegt: \begin{eqnarray}{\mathfrak{X}}={K}_{1}\cup {K}_{2}\cup \ldots\cup {K}_{k}\\ \,\,\,\,\,\text{mit}\,\,\,{K}_{k}\cap {K}_{j}=\Phi\,\,\,\text{f}\mathrm{\ddot{u}}\text{r}\,\,\,\,i\ne j.\end{eqnarray}

Anschließend werden die folgenden sogenannten Klassenhäufigkeiten der Stichprobendaten berechnet (j = 1, …n). \begin{eqnarray}\begin{array}{ll}{H}_{n}({K}_{i}) &-\text{Anzahl der Beobachtungen}\ {x}_{j}\ \text{mit}\ {x}_{j}\in \,{K}_{i}\\ {h}_{n}({K}_{i})=\frac{{H}_{n}({K}_{i})}{n} & -A\text{nteil der Beobachtungen}\,{x}_{j}\ \text{mit}\ {x}_{j}\in \,{K}_{i}\\ H(i)=\displaystyle {\sum }_{l=1}^{i}{H}_{n}({K}_{l})\, & -\text{Anzahl der}\,{x}_{j}\,\text{mit}\,{x}_{j}\le {a}_{i}^{o}\\ h(i)=\displaystyle {\sum }_{l=1}^{i}{h}_{n}({K}_{l})\,\, & -\text{Anzahl der}\,{x}_{j}\,\text{mit}\,{x}_{j}\le {a}_{i}^{o}\end{array}\end{eqnarray}

H_n(K_i) wird als absolute und h_n(K_i) als relative Klassenhäufigkeit bezeichnet. H(i) und h(i) sind die absoluten und relative Summenhäufigkeiten bzw. kurz die kumulativen Klassenhäufigkeiten. Die tabellarische Darstellung liefert die sogenannte Klassenhäufigkeitstabelle:

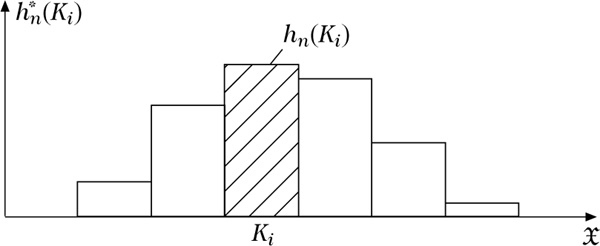
Die Gesamtheit der absoluten bzw. relativen Klassenhäufigkeiten H_n(K_i), i = 1, …, k bzw. h_n(K_i), i = 1, …, k ergibt die absolute bzw. relative Klassenhäufigkeitsverteilung; ihre graphische Darstellung bezeichnet man als Histogramm, siehe Abbildung 1.

Bei der Darstellung des Histogramms verwendet man zur Skalierung der y-Achse i. allg. die sogenannte relative Häufigkeitsdichte \begin{eqnarray}{h}_{n}^{* }({k}_{i})=\frac{{h}_{n}({K}_{i})}{\Delta{K}_{i}}\end{eqnarray} wobei \(\Delta{K}_{i}={a}_{i}^{0}-{a}_{i}^{u}\) die sog. Klassenbreite der Klasse K_i ist.

In diesem Fall ist die Fläche eines Balkens über der Klasse K_i gerade h_n(K_i) groß. Die Gesamtfläche unter den Balken beträgt 1.

Oft werden nach einer Klasseneinteilung die Stichprobendaten x₁, …, x_n vernichtet und nur die Klassenhäufigkeitstabelle aufbewahrt. Damit geht die Information über die einzelnen Beobachtungen verloren; man weiß nur noch, wieviele Daten in welcher Klasse liegen, aber nicht mehr, wie sie in einer Klasse verteilt sind. Unter der Modellannahme, daß die Stichprobendaten in jeder Klasse gleichmäßig verteilt sind, wird diese Tabelle zur Approximation der empirischen Verteilungsfunktion und der empirischen Momente wie Mittelwert und Streuung, sowie zur Approximation der empirischen Quantile von X herangezogen.

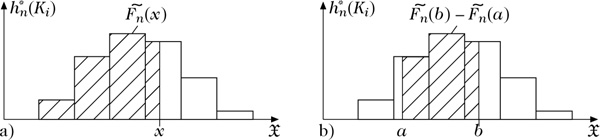
Seien \({a}_{j}^{u}\) die untere,\({a}_{j}^{o}\) die obere Klassengrenze und \({a}^{\prime}_{j}=\frac{{a}_{j}^{u}+{a}_{j}^{0}}{2}\) die Klassenmitte der Klasse K_j, dann wird die empirische Verteilungsfunktion F_n(x) wie folgt approximiert: \begin{eqnarray}\tilde{{F}_{n}}(x)=\left\{\begin{array}{ll}0, & \text{falls}\,x\lt {a}_{1}^{u},\\ h(i-1)+\frac{(x-{a}_{i}^{u})}{\Delta {K}_{i}} & \text{falls}\,x\in {K}_{i},\\ 1 & \text{falls}\,x\gt {a}_{k}^{0}.\end{array}\right.\end{eqnarray}

Unter der obigen Modellannnahme ist \(\tilde{{F}_{n}}(x)\) gleich dem Anteil aller x_j mit x_j ≤ x, siehe Abbildung 2a. Unter der obigen Modellanahme kann also das Histogramm als Schätzung der unbekannten Verteilungsdichte f(x) von X betrachtet werden (Dichteschätzung); die Fläche \(\tilde{{F}_{n}}(b)-\tilde{{F}_{n}}(a)\) unter den Balken zwischen a und b ist unter der obigen Modellannahme gleich dem Anteil aller Beobachtungen x_j mit a ≤ x_j ≤ b und wird dann als Schätzung der Wahrscheinlichkeit P(a ≤ X ≤ b) verwendet, siehe Abbildung 2b.

Das empirische α-Quantil wird aus dem Histogramm, d. h. unter Verwendung von \(\tilde{{F}_{n}}(x)\) geschätzt; aus der Definition des empirischen Quantils \begin{eqnarray}\tilde{{F}_{n}}({\tilde{x}}_{\alpha })=\alpha \end{eqnarray}

folgt nach Umstellung \begin{eqnarray}{\tilde{x}}_{\alpha }={a}_{1}^{u}+(\alpha -h(i-1))\Delta{K}_{i}\end{eqnarray} für 0 ≤ α ≤ 1.

Die Klasse K_i, in welcher das Quantil liegt, identifiziert man unter Benutzung der Häufigkeitstabelle; offensichtlich gilt \begin{eqnarray}{\tilde{x}}_{\alpha }\in {K}_{i}\,\text{genau dann, wenn}\,h(i-1)\lt \alpha \le h(i).\end{eqnarray}

Das arithmetische Mittel und die empirische Streuung werden approximiert durch \begin{eqnarray}\begin{array}{l}\tilde{x}=\displaystyle \sum _{i=1}^{k}{a}^{\prime}_{i}{h}_{n}({k}_{i}),\\ {\tilde{s}}^{2}=\frac{1}{n-1}\displaystyle \sum _{i=1}^{k}{({a}^{\prime}_{i}-\tilde{x})}^{2}{H}_{n}({k}_{i}).\end{array}\end{eqnarray}

Dabei ist die Approximation von s² durch \(\tilde{s}2\) abhängig von der Klassenbreite; in der Regel ist \(\tilde{s}2\) > s², weshalb in der deskriptiven Statistik bei konstanter Klassenbreite Δ := ΔK_i für alle i = 1, …, k anstelle von \({\tilde{s}}^{2}\) häufig die sogenannte Sheppardsche Korrekturformel \begin{eqnarray}{({s}^{* * })}^{2}={\tilde{s}}^{2}-\frac{{(\Delta K)}^{2}}{12}\end{eqnarray} verwendet wird.

Die Güte dieser nur unter Benutzung der Klassenhäufigkeitstabelle berechneten Schätzungen der Verteilungsfunktion, der Dichte, der Momente und der Quantile hängt wesentlich von der Wahl der Klassen, d. h. ihrer Lage (untere Grenze der ersten Klasse, deren Häufigkeit ungleich 0 ist), ihrer Zahl und ihrer Breite ab. Diese drei Werte werden in speziellen Anwendungen oft in Standards festgelegt. Man findet in der statistischen Literatur aber auch verschiedene allgemeine heuristische Regeln für die Wahl der drei Größen; so zum Beispiel die folgende:

Klassenzahl : \(k\approx \sqrt{n}\), (runden), mit der Forderung k ≥ 5.

Einzuteilender Bereich : B = [x_min − ε; x_max + ε], wobei ε so gewählt wird, daß möglichst kein Wert auf eine Klassengrenze fällt. Die untere Grenze der ersten Klasse mit Häufigkeit ungleich 0 ist dann \({a}_{i}^{u}={x}_{min}-\epsilon \)

Klassenbreite: \(\Delta{K}_{i}=\frac{B}{k}\), (aufrunden), i = 1 …, k.

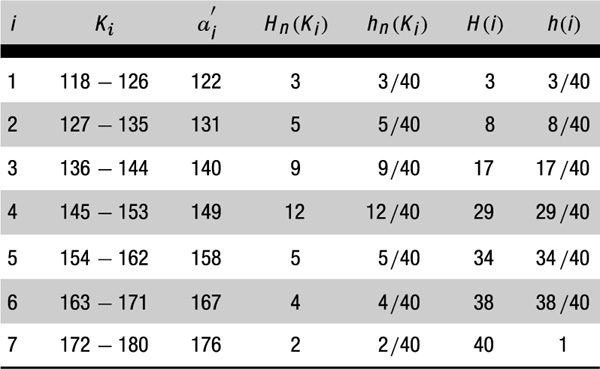
Beispiel. Bei der Produktion von Schrauben kommt es aufgrund der Technologie zu einer zufälligen Schwankung um eine gewünschte Normlänge von 150 mm. Es ist zu untersuchen, wie die Längen um die Norm schwanken. Dazu wurde eine Stichprobe von 40 Schrauben gemessen; es ergaben sich folgende Längen (in mm): \begin{eqnarray}138 \,\, & \,\, 164 \,\, & \,\, 150 \,\, & \,\, 132 \,\, & \,\, 144 \,\, & \,\, 125 \,\, & \,\, 149 \,\, & \,\, 157\\ 146 \,\, & \,\, 158 \,\, & \,\, 140 \,\, & \,\, 147 \,\, & \,\, 136 \,\, & \,\, 148 \,\, & \,\, 152 \,\, & \,\, 144\\ 168 \,\, & \,\, 126 \,\, & \,\, 138 \,\, & \,\, 178 \,\, & \,\, 163 \,\, & \,\, 119 \,\, & \,\, 154 \,\, & \,\, 165\\ 146 \,\, & \,\, 173 \,\, & \,\, 142 \,\, & \,\, 147 \,\, & \,\, 135 \,\, & \,\, 156 \,\, & \,\, 140 \,\, & \,\, 135\\ 161 \,\, & \,\, 145 \,\, & \,\, 135 \,\, & \,\, 142 \,\, & \,\, 150 \,\, & \,\, 156 \,\, & \,\, 145 \,\, & \,\, 128\end{eqnarray}

Hieraus erhalten wir in Anwendung der o. g. Empfehlungen zur Bildung der Klassen: \begin{eqnarray}\begin{array}{ll}\text{Klassenzahl}:\,\, & \sqrt{n}=\sqrt{40}=6,33,\to k=7\\ \text{Einzuteilender}\ \text{Bereich}: & {x}_{\min }=119,\,{x}_{\max }=176.\, \text{Wir w}\mathrm{\ddot{a}}\text{hlen}\ \varepsilon =\ 1,\ \text{d}.\ \text{h}.,\\ & \text{wir}\ \text{zerlegen den Bereich von}\ 118\ -177\ \text{in}\ 7\ \text{Klassen}.\\ \text{Klassenbreite}: & \Delta K=\frac{177-118}{7}=8,4\,\to \,\Delta K=9.\end{array}\end{eqnarray}

Wir erhalten damit folgende Klassenhäufigkeitstabelle:

Nachdem die Klassenhäufigkeitstabelle erstellt wurde, wurden die 40 Originalbeobachtungsdaten vernichtet. Es sollen nun nur unter Benutzung der vorliegenden Häufigkeitstabelle das arithmetische Mittel, die empirische Streuung, die beiden Quantile \({\tilde{x}}_{0,25}\) und \({\tilde{x}}_{0,75}\) (die sogenannten Quartile), sowie der Anteil der Schrauben (an der Stichprobe) bestimmt werden, die eine Länge zwischen 140 und 160 mm besitzen. Es ergibt sich: \begin{eqnarray}\begin{array}{ll}\tilde{x}= & \frac{122\,\cdot\, 3+131\,\cdot\, 5+140\,\cdot\, 9+149\,\cdot\, 12}{40}+\\ & +\frac{158\,\cdot\, 5+167\,\cdot\, 4+176\,\cdot\, 2}{40}=146,975,\end{array}\\ \begin{array}{ll}{\tilde{s}}^{2}= & \frac{1}{39}[{(122-(\tilde{x}))}^{2}\,\cdot\, 3+{(131-\tilde{x})}^{2}\,\cdot\, 5+\\ & +{(140-\tilde{x})}^{2}\,\cdot\, 9+{(149-\tilde{x})}^{2}\,\cdot\, 12+\\ & +{(158-\tilde{x})}^{2}\,\cdot\, 5+{(167-\tilde{x})}^{2}\,\cdot\, 4+\\ & +{(176-\tilde{x})}^{2}\,\cdot\, 2]=193,102,\end{array}\end{eqnarray} sowie \begin{eqnarray}{({s}^{* * })}^{2}=193,102-\frac{{9}^{2}}{12}=186,\,352.\end{eqnarray}

Weiterhin sind \begin{eqnarray}{\tilde{x}}_{0,25}\in {K}_{3}(i=3),\, & \text{da}\,\,\,8/40\ \lt \,0,25\,\lt \,17/40,\\ {\tilde{x}}_{0,75}\in {K}_{5}(i=5),\,\, & \text{da}\,\,\,29/40\ \lt \,0,75\,\lt \,34/40,\end{eqnarray}\begin{eqnarray}\begin{array}{lll}{\tilde{x}}_{0,25} & = & {a}_{3}^{u}+(0,25-h(2))\Delta K\\ & = & 136+(0,25-8/40)\cdot 9\\ & = & 136+0,05\cdot 9=136,45\end{array}\\ \begin{array}{lll}{\tilde{x}}_{0,75} & = & {a}_{5}^{u}+(0,75-h(4))\Delta K\\ & = & 154+(0,75-29/40)\cdot 9\\ & = & 154+0,025\cdot 9=154,225.\end{array}\end{eqnarray}

Für den Anteil der Schrauben, deren Länge im Intervall [140, 160] mm liegt, gilt schließlich (160 ∈ K₅(i = 5), 140 ∈ K₃(i = 3)): \begin{eqnarray}{\tilde{F}}_{n}(160)-{\tilde{F}}_{n}(140) & = & h(4)+\frac{160-154}{9}-h(2)-\frac{140-136}{9}\\ & = & 29/40+6/9-8/40-4/9=21/40+2/9\\ & = & 289/360=0,803.\end{eqnarray}

Mit diesen Daten kann man jetzt einen χ^2-Anpassungstest zum Prüfen der zufälligen Länge auf Normalverteilung, die Berechnung von Konfidenzintervallen (Bereichsschätzung) für den unbekannten Erwartungswert und für die unbekannte Varianz der Länge aller Schrauben der Gesamtprodunktion, sowie die Berechnung eines Konfidenzintervalls für die unbekannte Ausschußrate, d. h. den Anteil aller Schrauben an der Gesamtproduktion, die nicht im Intervall [140, 160] liegen, anschlie-ßen (Box-Plot).

Literatur

[1] Schwarze,J.: Grundlagen der Statistik I – Beschreibende Verfahren. Verlag Neue Wirtschafts-Briefe Herne/Berlin, 1990.