Lexikon der Mathematik: Methode der kleinsten Quadrate
Verfahren zur Lösung eines überbestimmten Systems von N Gleichungen zur Bestimmung von n Unbekannten x1, x2, …, xn aus N beobachteten Meßwerten
Typischerweise kann ein solches überbestimmtes Gleichungssystem nicht exakt gelöst werden. Stattdessen versucht man bei der Methode der kleinsten Quadrate, eine Lösung x1, x2, …, xn so zu bestimmen, daß die Summe der Quadrate der in den einzelnen Gleichungen auftretenden Abweichungen
minimal ist. Mit anderen Worten: Mit r = (r1, r2,…, rN)T ∈ ℝN minimiere
Die notwendige Bedingungen zur Minimierung der Funktion F sind dann gerade
d. h., der Gradient von F muß verschwinden.
Sind die Funktionen gi nichtlinear in den xj, so ergibt sich ein System von n nichtlinearen Gleichungen, welches nur schwer zu lösen ist. Man verwendet hier dann häufig die Gauß-Newton-Methode zur Lösung. Sind die Funktionen gi hingegen linear in den xj,
(wobei die aik Skalare oder Funktionen sein können), so erhält man mit \(A={({a}_{ik})}_{i=1,\mathrm{...},N}^{k=1,\mathrm{...},n}\) und ℓ = (ℓ1, ℓ2, …, ℓN)T ∈ ℝN
und als notwendige Bedingung für ein Minimum von F die Normalgleichungen
Da ATA eine symmetrische Matrix ist, kann die Normalgleichung mittels des Cholesky-Verfahrens gelöst werden. Bei der Lösung der Normalgleichung können numerische Probleme auftreten, wenn die Konditionszahl der Matrix ATA sehr groß ist. Die Lösung x hat dann relativ große Fehler. Zudem sind Rundungsfehler bereits bei der Berechnung von ATA und ATℓ Berechnung vo unvermeidlich.
Numerisch besser ist es, das zu min rTr äquivalente Ausgleichsproblem
zu betrachten und dieses mittels der QR-Zerlegung von A zu lösen. Berechnet man die QR-Zerlegung von A = QR, so gilt
da Q eine orthogonale Matrix ist. Hat A vollen Spaltenrang, d. h. Rang(A) = n, dann hat R ∈ ℝ
mit einer oberen Dreiecksmatrix \(\hat{R}\in {{\mathbb{R}}}^{n\times n}\). Setzt man
dann folgt
Dieser Ausdruck wird minimal für x ∈ ℝn mit \(\hat{R}x=b\). Dieses x läßt sch leicht durch Rückwärtseinsetzen gewinnen.
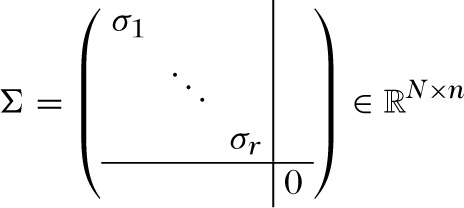
Hat A nicht vollen Spaltenrang, d. h. Rang(A) = r < n, dann existieren unendlich viele Lösungen des Ausgleichsproblems \(\mathop{\min }\limits_{x}|| {\ell} -Ax|{|}_{2}^{2}\). In diesem Fall wählt man i. allg. unter allen minimierenden Lösungen x diejenige mit kleinster 2-Norm als Lösung des Ausgleichsproblems. Zur Berechnung verwendet man die Singulärwertzerlegung A = UΣVT, wobei U ∈ ℝ
ist. Schreibt man U = (u1, …, uN), uj ∈ ℝN und V = (v1, …, vn), vj ∈ ℝn, dann minimiert
gerade \(|| {\ell} -Ax|{|}_{2}^{2}\) und hat die kleinste 2-Norm aller minimierenden Lösungen.
Die Methode der kleinsten Quadrate geht auf Gauß zurück und fand zunächst vorwiegend in der Ausgleichsrechnung Verwendung. Die Grundaufgabe der Ausgleichsrechnung besteht darin, an N Punkte (xi, yi), i = 1, …, n, der Ebene eine Funktion \(f(x;\overrightarrow{\gamma })\), x ∈ ℝ1, die bis auf k unbekannte Parameter \(\overrightarrow{\gamma }=({\gamma }_{1},\mathrm{...},{\gamma }_{k})\in {{\mathbb{R}}}^{k}\), k < n, vollständig gegeben ist, möglichst gut durch geeignete Wahl der Parameter \(\overrightarrow{\gamma }\) anzupassen. Die Methode fand Einzug in die mathematische Statistik, als R.A.Fisher die Maximum-Likelihood-Methode eingeführt und ihren Zusammenhang zur Methode der kleinsten Quadrate hergestellt hat. Sie wird hier vor allem in der Regressionsanalyse zur Konstruktion von Punktschätzungen für die Parameter der Ausgleichsfunktion, die in der Regressions-analyse als Regressionsfunktion bezeichnet wird, angewendet.
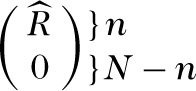
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.