Gaußsche Abbildung, Gaußsche Kollineation, kollineare Abbildung, mathematische eindeutige und eindeutig umkehrbare, durch eine gebrochene lineare Funktion beschreibbare Ähnlichkeitstransformation konjugierter Größen, die geometrisch einer projektiven Abbildung von Objektpunkten in Bildpunkte entspricht. Da kollineare, d.h. auf einer Geraden liegende bzw. komplanare, d.h. auf einer Ebene liegende Punkte wieder in kollineare bzw. komplanare Punkte abgebildet werden, werden Geraden in Geraden und Ebenen in Ebenen abgebildet. Die Brennebenen sind zu unendlich fernen Ebenen konjugiert.

Die G. A. läßt sich strahlengeometrisch konstruieren (Bildkonstruktion), wobei sich alle von einem Objektpunkte ausgehenden Strahlen wieder im konjugierten Gaußschen Bildpunkt schneiden. Die Strahlen der G. A. sind nur geometrische Konstruktionslinien, die nicht den Lichtstrahlen eines die G. A. als optischer Analogrechner mit Aberrationen unvollkommen durch optische Abbildung simulierenden optischen Systems entsprechen.

Nur der wichtige Spezialfall der zentrierten, d.h. axialsymmetrischen G. A., bei der die Bildkonstruktion über die Strahlabknickung an den mit dem Abbildungsmaßstab β'_H=1 aufeinander abgebildeten Hauptebenen erfolgt, entspricht der paraxialen optischen Abbildung. Die Hauptebenen repräsentieren bei diesem als Gaußsche Dioptrik bezeichneten einfachsten, abstrakten, die Eigenschaften des Lichtes nicht berücksichtigenden Modell der optischen Abbildung das optische System, wobei aber zu beachten ist, daß sie auch außerhalb der Systeme liegen können (Abb. 1b). Zusammen mit den Hauptebenen bilden die Hauptpunkte H und H' als deren Achsenpunkte, das Interstitiumi=HH', die Brennebenen und als deren Achsenpunkte die Brennpunkte

und F', die Brennweiten

und f' als die Brennpunktsabstände von den Hauptpunkten, die in den Hauptpunktsabständen 2

und 2f' angeordneten, mit dem Abbildungsmaßstab β'_N=-1 aufeinander abgebildeten negativen Hauptebenen, deren Achsenpunkte die negativen Hauptpunkte N und N' sind, die Knotenpunkte K und K', die in den Abständen f' und

von

und F' liegen und durch die die Strahlen ohne Richtungsänderung, d.h. mit der Winkelvergrößerung γ'_K=1 verlaufen, der Dingpunkt und der Gaußsche Bildpunkt O und O', die Objektebene und die Gaußsche Bildebene, die Objekt- und die Bildweitea und a' als deren Hauptebenenabstände, die Brennpunktsabstände z und z' der Objekt- und der Bildebene und die Symmetrieachse die Kardinalelemente der axialsymmetrischen G. A. (Abb. 1a).

Die Abbildungsgleichungen der axialsymmetrischen G. A. sind die Newtonsche Abbildungsgleichung

bzw. die Linsengleichung

und die daraus abgeleitete Relation

zwischen der Objekt- und der Bildhöhe y und y'. Wegen der Ortsabhängigkeit des lateralen Abbildungsmaßstabes β' und dessen Nichtübereinstimmung mit dem Tiefenabbildungsmaßstab

ist die axialsymmetrische G. A. nicht volumentreu, sondern perspektivisch verzeichnet (Abb. 1c).

Mit Hilfe der Höhenverhältnisse ω_i lassen sich Κ zu einer gemeinsamen Achse symmetrische G. A. i mit den objekt- und bildseitigen Brechkräften

zu einer resultierenden axialsymmetrischen G. A. mit der Brechkraft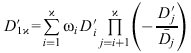

zusammenfassen. Für den Übergang zwischen den G. A. i und i+1 mit den Haupt- bzw. Brennpunktsabständen

bzw.

(optische Tubuslänge) gelten die Transformationen

und

(Abb. 2). Die zusammengesetzte G. A. ist die Basis der Theorie der optischen Instrumente und des Brechtkraftansatzes für optische Systeme.

Ein Resultat der G. A. ist die Scheimpflug-Bedingung. Aus der Diskrepanz zwischen G. A. und geometrischer Optik ergeben sich die geometrisch-optischen Aberrationen. Die G. A. stimmt nur im paraxialen Gebiet mit der aplanatischen Abbildung überein.

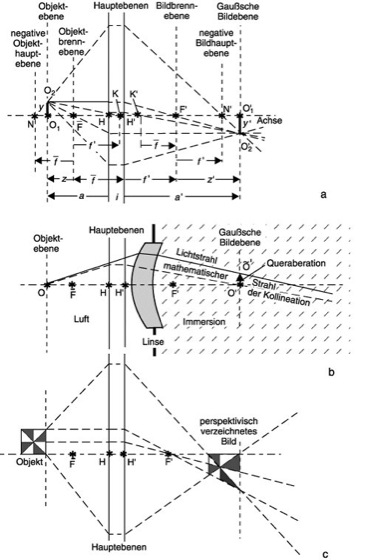
Gaußsche Abbildung 1: Kardinalelemente und Strahlenverlauf bei der Gaußschen Abbildung (a), Vergleich des Strahlenverlaufs bei der Gaußschen und bei der optischen Abbildung durch einen Meniskus mit Immersion im Bildraum (b) und perspektivische Verzeichnung bei der Gaußschen Abbildung räumlicher Objekte (c). H und H' Hauptpunkte, N und N' negative Hauptpunkte,

und F' Brennpunkte, K und K' Knotenpunkte,

und f' Brennweiten, a Objekt- und a'' Bildweite, i Interstitium.

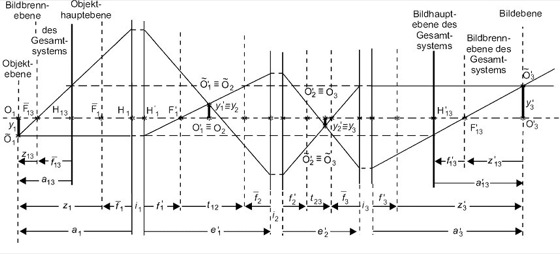
Gaußsche Abbildung 2: Eine aus 3 einzelnen Gaußschen Abbildungen zusammengesetzte Gaußsche Abbildung.