Sphärometer, Gerät zur Messung der Krümmungsradien von sphärisch gekrümmten Flächen. Dies kann sowohl mechanisch als auch optisch-mechanisch erfolgen.

1) Mechanische S. Es wird eine Pfeilhöhe eines Kugelsegmentes gemessen und aus dem Segmentradius r und der Pfeilhöhe h der Krümmungsradius R nach der Formel R=(r²+h²)/2h berechnet (Abb. 1).

Die zu untersuchende Linsenfläche wird dabei entweder auf zwei oder drei Spitzen oder auf einem Ring gelagert. Die Bestimmung der Pfeilhöhe erfolgt mit einem Taster, dessen Verschiebung gemessen wird. Der Taster befindet sich in der Mitte des Ringes oder der Spitzen. Als Bezugsfläche wird meist eine Planfläche benutzt.

Eine einfache Ausführungsform ist das Dreifußsphärometer. Es besitzt drei Spitzen, die auf die Fläche gesetzt werden, und eine Mikrometerschraube oder eine Meßuhr mit Meßspitze zur Bestimmung der Pfeilhöhe. Die Pfeilhöhe wird dabei im allgemeinen auf 0,01 mm genau angezeigt.

Für genaue Messungen benutzt man Präzisionssphärometer mit einem Satz verschieden großer Meßringe. Die Pfeilhöhe wird mit einem Tastbolzen gemessen, dessen Verschiebung mit einem Wegmeßsystem erfaßt wird, das eine Auflösung von z.B. 0,001 mm hat.

2) Kombinierte optisch-mechanische Verfahren. Dabei wird der Krümmungsmittelpunkt der zu messenden Fläche ermittelt und der Krümmungsradius direkt gemessen als Strecke vom Krümmungsmittelpunkt zum Flächenscheitel. Die Messung erfolgt mit einem geeigneten Wegmeßsystem. Der Krümmungsmittelpunkt kann z.B. bei Konkavflächen mit dem Foucaultschen Schneidenverfahren (Objektivprüfung) oder mittels eines Autokollimationsokulars ermittelt werden.

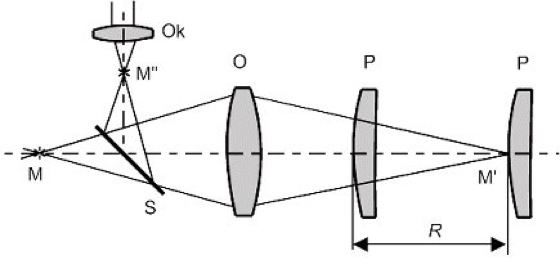
Bei dem Autokollimationssphärometer wird durch ein Objektiv O eine beleuchtete Meßmarke M (Fadenkreuz) in endlicher Entfernung, am Orte M', abgebildet (Abb. 2). Die zu messende Fläche wird als Spiegelfläche verwendet, die die Strahlen wieder zurück in das Objektiv reflektiert. Unter bestimmten Bedingungen entsteht ein Bild der Marke an ihrem Ursprungsort oder nach Reflexion an einem teildurchlässigen Spiegel S an einem korrespondierenden Ort M″. Dort wird das Bild durch ein Okular Ok scharf gesehen, wenn Scheitel oder Krümmungsmittelpunkt der zu messenden Fläche mit dem Ort M' zusammenfällt. Bei den Autokollimationssphärometern wird entweder der Prüfling oder der Autokollimationskopf verschoben und die Verschiebung gemessen. Die zwischen den zwei Stellungen mit scharfer Abbildung auftretende Verschiebung entspricht dem zu messenden Krümmungsradius.

Für die Messung großer Krümmungsradien ist auch ein normales Autokollimationsfernrohr (technische Fernrohre) geeignet. Der Prüfling wird in den vorderen Brennpunkt des Fernrohrobjektivs gebracht und der Okularauszug (einschließlich Autokollimationsmarke und Fadenkreuz) so lange verstellt, bis die Marke scharf und parallaxenfrei in der Ebene des Fadenkreuzes im Okular gesehen wird. Das Fernrohr ist in diesem Fall auf den Krümmungsmittelpunkt der Fläche eingestellt. Muß dabei der Okularauszug um die Strecke a aus der Einstellung auf ∞ (Kontrolle mit gutem Planspiegel) verstellt werden, so ergibt sich der Radius zu R=f²/a, wobei f die Brennweite des Fernrohrobjektivs bedeutet.

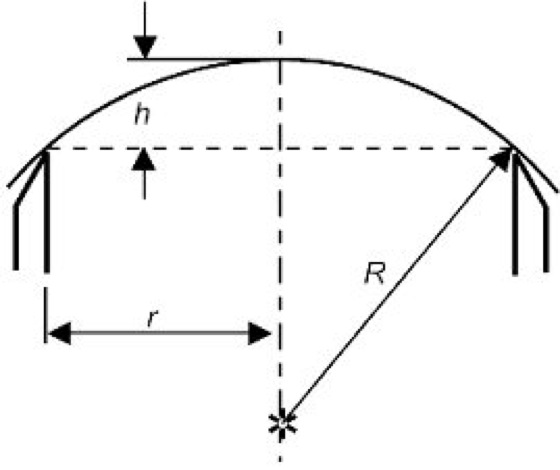
Sphärometer 1: Bestimmung des Krümmungsradius R aus dem Auflageradius r und der Pfeilhöhe h.

Sphärometer 2: Autokollimationssphärometer. M Meßmarke; M', M″ die Orte von deren Bildern, O Objektiv, P Prüfling, S halbdurchlässiger Spiegel, Ok Okular.