Lexikon der Mathematik: Arcuscosekansfunktion
Areuseosekans, die aufgrund der Bijektivität der Cosekansfunktion
\begin{eqnarray}\csc :[-\frac{\pi }{2},\frac{\pi }{2}]\backslash \{0\}\to {\rm{{\mathbb{R}}}}\backslash (-1,1)\end{eqnarray}
\begin{eqnarray}\mathrm{arccsc}:{\rm{{\mathbb{R}}}}\backslash (-1,1)\to [-\frac{\pi }{2},\frac{\pi }{2}]\backslash \{0\}.\end{eqnarray}
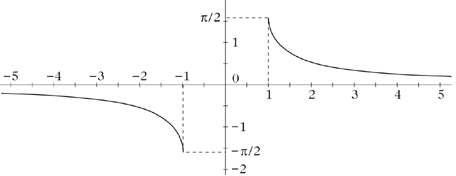
arccsc
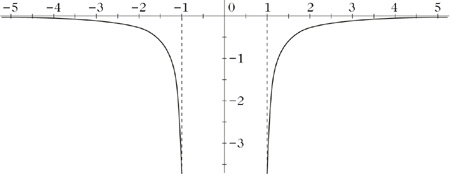
arccsc’
Für x ∈ ℝ \ {kπ | k ∈ ℤ} und y ∈ ℝ \ (–1, 1) gilt genau dann csc x = y, wenn
\begin{eqnarray}x=\mathrm{arccsc}y+2k\pi \mathrm{oder}x=(2k+1)\pi -\mathrm{arccsc}y\end{eqnarray}
Mit csc ist auch arccsc eine ungerade Funktion. Nach dem Satz über die Differentiation der Umkehrfunktion ist arccsc differenzierbar in ℝ \ [−1, 1], und für y ∈ℝ \ [−1, 1] gilt
\begin{eqnarray}{\mathrm{arccsc}}^{^{\prime} }(y)=-\frac{1}{|y|\sqrt{{y}^{2}-1}}.\end{eqnarray}
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.