Lexikon der Mathematik: Differentiation der Umkehrfunktion
ist möglich an den Stellen, an denen die Funktion selbst differenzierbar und ihre Ableitung verschieden von Null ist.
Genauer: Ist f : I → ℝ eine auf einem Intervall I ⊂ ℝ definierte, streng isotone oder streng antitone stetige Funktion, die an einer Stelle a ∈ I differenzierbar ist mit f′(a) ≠ 0, dann ist ihre (wegen der strengen Monotonie existierende) Umkehrfunktion f−1 differenzierbar in f(a) mit
Man erkennt dies auch unmittelbar durch Betrachten des Graphen von f (vgl. Abbildung): Der Über-gang von f zu f−1 entspricht einer Spiegelung an der Hauptdiagonalen, weshalb die Steigung von f−1 an der Stelle f(a) sich aus der von f an der Stelle a durch Kehrwertbildung ergibt.
Weiß man, daß die Funktion f−1 in f(a) differenzierbar ist, so liefert auch die Kettenregel die Formel zur Berechnung ihrer Ableitung: Es gilt nämlich x = (f−1 ∘ f)(x) für x ∈ I, also
Zur Differentiation der Umkehrfunktion
Zum Beispiel ist die Funktion sin : \([-\frac{\pi }{2},\frac{\pi }{2}]\to \) [−1, 1] differenzierbar, streng isoton und surjektiv, und es ist sin′ = cos. Somit gilt für die Umkehrfunktion arcsin : \([-1,1]\to [-\frac{\pi }{2},\frac{\pi }{2}]\) für y ∈ (−1, 1)
Bei f′(a) < 0 bzw. f′(a) > 0 und Stetigkeit von f′ in a ist f in einer Umgebung von a streng antiton bzw. isoton. Daher gilt: Ist f : I → ℝ eine auf einem Intervall I ⊂ ℝ definierte differenzierbare Funktion, und ist f′ stetig in a mit f′(a) ≠ 0, dann gibt es eine Umgebung U von a so, daß die Einschränkung f/U : U → f(U) bijektiv ist und f′(x) ≠ 0 gilt für x ∈ U.
Die Umkehrfunktion \({f}_{/U}^{-1}\) ist differenzierbar, und es gilt
Ist f : G → ℝn eine auf einer offenen Menge G ⊂ ℝn definierte stetig differenzierbare Abbil-dung, die an der Stelle a ∈ G eine invertierbare Ableitung f′(a) besitzt, dann gibt es eine offene Umgebung U ⊂ G von a so, daß f(U) eine offene Umgebung von f(a) und die Einschränkung f/U : U → f(U) bijektiv ist und f′(x) invertierbar für x ∈ U.
Die Umkehrfunktion
Verallgemeinerungen dieses Satzes liefern Aussagen über Ck-Diffeomorphismen.
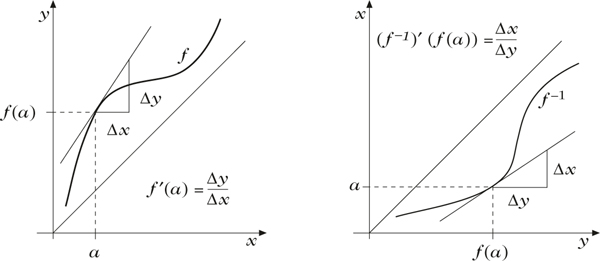
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.