Lexikon der Mathematik: blossoming
ein Prozeß, der im einfachsten Fall einer Splinefunktion \(b:[a,b]\to {{\mathbb{R}}}^{1}\) oder einer B-Splinekurve \(b:[a,b]\to {{\mathbb{R}}}^{n}\) der Ordnung m, die durch die Kontrollpunkteb0, …, br und den Knotenvektor \({x}_{1},\ldots, {x}_{r+m+1}\) festgelegt ist, die multi-affinen Polarformen Bj der Polynomfunktionen \(b|({x}_{j},{x}_{j+1})\) zuweist, sofern dieses Intervall nicht leer ist.
Die Polarformen \({B}_{j}({t}_{1},\ldots, {t}_{m})\) haben die folgenden Eigenschaften:
- Eine Permutation der Argumente \({x}_{1},\ldots, {x}_{m}\) ändert den Wert von B nicht (1).
- Für alle α, t1, t2, ⋯, ∈ ℝ gilt
\begin{eqnarray}\alpha {B}_{j}(\ldots {t}_{i}\ldots )+(1-\alpha ){B}_{j}(\ldots {t}_{i}^{^{\prime} }\ldots )\\ ={B}_{j}(\ldots, \alpha {t}_{i}+(1-\alpha ){t}_{i}^{^{\prime} },\ldots ),\end{eqnarray}
\begin{eqnarray}{B}_{j}(t,\ldots, t)=b(t)\text{f}\mathop{\text{u}}\limits^{\mathrm{..}}\text{r}\text{\hspace{0.17em}}t\in [{x}_{j},{x}_{j+1}],\end{eqnarray}
\begin{eqnarray}{b}_{l}={B}_{j}({x}_{l+1},\ldots, {x}_{l+m})\text{\hspace{0.17em}}\text{f}\mathop{\text{u}}\limits^{\mathrm{..}}\text{r}\text{\hspace{0.17em}}l\le j\le l+m.\end{eqnarray}
\begin{eqnarray}{B}_{j-1}(\star )={B}_{j}(\star )\text{f}\mathop{\text{u}}\limits^{\mathrm{..}}\text{r}\text{\hspace{0.17em}}\star =(\mathop{\underbrace{{x}_{j}\ldots {x}_{j}}}\limits_{{}_{(m-r)\times }},{t}_{r+1},\ldots ).\end{eqnarray}
(4) zeigt, wie man bei gegebenen Polarformen die Kontrollpunkte rekonstruiert und ist ein Beweis dafür, daß jede Splinefunktion eine Linearkombination der normalisierten B-Splinefunktionen ist.
(3) gemeinsam mit (1) und (2) erlaubt es, die B-Splinekurve an einer Stelle t auszuwerten. Eine darauf beruhende Rekursionsformel zur Auswertung ist der de Boor-Algorithmus.
Wegen (5) kann man die Polarformen Bj zu einer einzigen Abbildung B aus \({{\mathbb{R}}}^{m}\) in \({{\mathbb{R}}}^{n}\) zusam-menkleben. Wenn ein Knoten unter den Argumenten vorkommt, ist es innerhalb gewisser Grenzen gleichgültig, welche der Polarformen \({B}_{j}\) man zur Auswertung heranzieht.
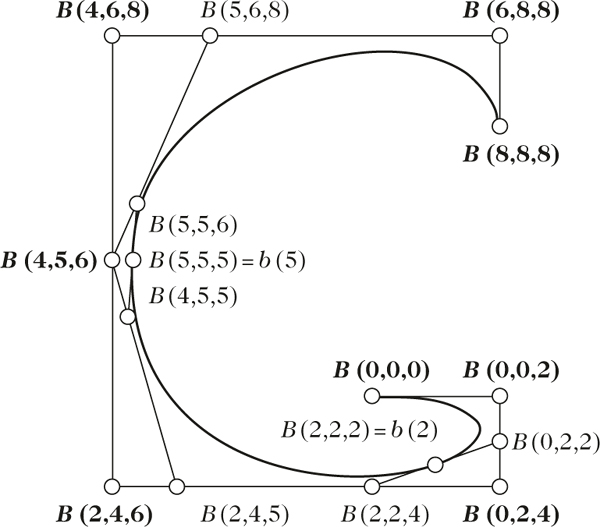
B-Splinekurve 3. Ordnung über dem Knotenvektor 0, 0, 0, 2, 4, 6, 8, 8, 8 mit blossom.
Das ist auch mit der folgenden geometrischen Eigenschaft des blossoms verknüpft: Für zulässige Argumente liegt der Punkt \(B({t}_{1},\ldots, {t}_{m})\) in der sog. \((m-1)\)-Schmiegebene der Kurve b an den Stellen \({t}_{1},\ldots, {t}_{m}\). Kommt ein Argument mehrfach vor, z. B. \({t}_{1}=\ldots ={t}_{r}\), so liegt \(B({t}_{1},\ldots, {t}_{m})\) in der \((m-r)\)-Schmiegebene von b an der Stelle t.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.