Lexikon der Mathematik: orthogonale Polynome
ein System von polynomialen, u. U. noch nicht normierten Elementen eines vollständigen Orthonormalsystems eines Funktionen-Hilbertraumes.
Genauer gilt: Eine Familie von Polynomen {pn}n∈ℕ vom Grade grad pn = n heißt eine Familie von orthogonalen Polynomen auf dem Intervall [a, b] ⊂ ℝ bezüglich des Gewichtes w, w(x) ≥ 0, wenn
Das Gewicht sowie das Intervall bestimmen die Polynome bereits eindeutig bis auf einen konstanten Faktor.
Derartige Polynome bilden im Hilbertraum L2([a, b], w(x) dx), definiert durch das Skalarprodukt
Führt man die Bezeichnungen
Die Polynome lassen sich auch vermöge der Rodrigues-Formel
Betrachtet man z. B. den Hilbertraum L2([−1, +1], dx) mit dem Skalarprodukt
Auf dem Hilbertraum \({L}^{2}({\mathbb{R}},{e}^{-{x}^{2}}dx)\) bilden die Hermite-Polynome orthogonale Polynome, sie werden u. a. in der Quantenmechanik zur Lösung des harmonischen Oszillators benutzt und sind Spezialfälle der parabolischen Zylinderfunktionen. Andere Anwendungen finden sich in der Statistik.
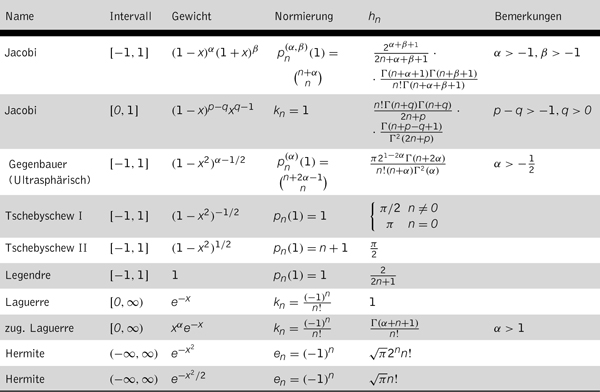
Tabelle 1: Orthogonale Polynome
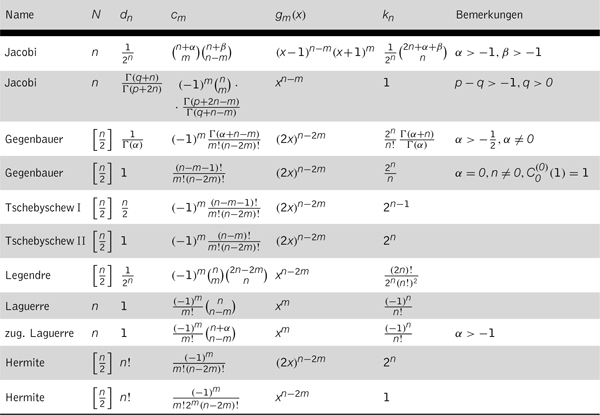
Tabelle 2: Explizite Darstellungen orthogonaler Polynome
Die Tschebyschew-Polynome
Die Laguerre-Polynome auf [0, ∞) mit den Gewichten w(x) = e−x bzw. w(x) = xαe−x finden sich z. B. wieder in der Quantenmechanik zur Konstruktion von Lösungen des Wasserstoff-Atoms, ferner zur Beschreibung der Geschwindigkeitsverteilung in der kinetischen Gastheorie.
Für weitere Information über diese orthogonalen Polynome vergleiche man auch die jeweiligen Stichworteinträge. Weitere orthogonale Polynome findet man in Tabelle 1, explizite Entwicklungen in der Form
[1] Abramowitz, M.; Stegun, I.A.: Handbook of Mathematical Functions. Dover Publications, 1972.
[2] Olver, F.W.J.: Asymptotics and Special Functions. Academic Press, 1974.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.