elliptische Funktionen mit jeweils zwei einfachen Polen in ihrem Fundamentalbereich. Leider finden sich vielfältige Konventionen bei der Definition dieser Funktionen, hier soll größtenteils [1] gefolgt werden.

Seien κ und κ′ zwei reelle Zahlen mit κ² +κ′² = 1. Man nennt κ auch den Modul, κ′ das Komplement des Moduls. Man definiere nun die Viertelperioden K und K′ durch \begin{eqnarray}\begin{array}{rll}\text{K} & := & \displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\vartheta }{(1-{\kappa }^{2}\,{\sin }^{2}\,\vartheta },\\ {\text K}{^{\prime} } & := & \displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\vartheta }{(1-{{\kappa }{^{\prime} }}^{2}\,{\sin }^{2}\,\vartheta }.\end{array}\end{eqnarray}

Die Zahlen K′ und iK′ spannen in der komplexen Zahlenebene das Rechteckgitter \begin{eqnarray}\begin{array}{cc}\Gamma :=n\text{K}+im{\text K}{^{\prime} } & (n,m\in {\mathbb{Z}})\end{array}\end{eqnarray} auf. Die Eckpunkte dieses Gitters sollen nun gemäß der Abbildung mit den Buchstaben s, c, d und n versehen werden; hierbei ensteht dann das sog. Argand-Diagramm.

Die Jacobi-Funktion pq, wobei p und q jeweils einen der Buchstaben s, c, d und n vertritt, ist diejenige elliptische Funktion, die

• einfache Nullstellen an den Punkten p und einfache Pole an den Punkten q im Argand-Diagramm besitzt, und
• die Perioden 4K und 4iK′ sowie 2(p − q) besitzt. Dadurch ist die Funktion pq bereits eindeutig definiert. Will man die Abhängigkeit vom Modul κ betonen, so schreibt man auch pq (ζ|κ) statt pq (z).

Historisch wurden die Jacobischen elliptischen Funktionen allerdings anders eingeführt. Man vergleiche hierzu das Stichwort Amplitudinisfunk- tion.

Normalerweise kommt man mit einem Satz von drei elementaren Funktionen, sn, cn und dn aus, denn für die restlichen Funktionen findet man folgende Zusammenhänge: \begin{eqnarray}\begin{array}{l}\text{cd}=\frac{\text{cn}}{\text{dn}}\quad\text{dc}=\frac{\text{dn}}{\text{cn}}\quad\text{ns}=\frac{1}{\text{sn}}\\ \text{sd}=\frac{\text{sn}}{\text{dn}}\quad\text{nc}=\frac{1}{\text{cn}}\quad\text{ds}=\frac{\text{dn}}{\text{sn}}\\ \text{nd}=\frac{1}{\text{dn}}\quad\text{sc}=\frac{\text{sn}}{\text{cn}}\quad\text{cs}=\frac{\text{cn}}{\text{sn}}\end{array}\end{eqnarray} Gelegendlich findet man die Funktion dn auch als Δ bezeichnet.

Wie jede elliptische Funktion lassen sich auch die Funktionen sn, cn und dn durch die Weierstraßsche ℘-Funktion oder auch durch Weierstraßsche σ-Funktionen ausdrücken. Bezeichnet man die Perioden der ℘-Funktion mit ω und ω′, definiert ferner \begin{eqnarray}\begin{array}{llll}{\omega }_{1}:=\omega, & {\omega }_{2}:=\omega +{\omega }{^{\prime} }, & {\omega }_{3}:={\omega }{^{\prime} }, & {e}_{i}:=\wp ({\omega }_{i}),\end{array}\end{eqnarray} und wählt \begin{eqnarray}{\kappa }^{2}:=\frac{{e}_{2}-{e}_{3}}{{e}_{1}-{e}_{3}},\quad{{\kappa }{^{\prime} }}^{2}=\frac{{e}_{1}-{e}_{2}}{{e}_{1}-{e}_{3}},\end{eqnarray} und \begin{eqnarray}u:={({e}_{1}-{e}_{3})}^{1/2}z,\end{eqnarray} so gilt: \begin{eqnarray}\begin{array}{lll}\text{sn}\,(u,\kappa ) & = & \frac{{({e}_{1}-{e}_{3})}^{1/2}}{{(\wp (z)-{e}_{3})}^{1/2}}\\ & = & {({e}_{1}-{e}_{3})}^{1/2}\frac{\sigma (z)\sigma ({\omega }_{3})}{\sigma ({\omega }_{3}-z)}{e}^{-{\eta }_{3}z}\end{array}\end{eqnarray}\begin{eqnarray}\begin{array}{lll}\text{cn}(u,k) & = & \frac{{(\wp (z)-{e}_{1})}^{1/2}}{{(\wp (z)-{e}_{3})}^{1/2}}\\ & = & \frac{\sigma ({\omega }_{1}-z)\sigma ({\omega }_{3})}{\sigma ({\omega }_{3}-z)\sigma ({\omega }_{1})}{e}^{-{\eta }_{3}z+{\eta }_{1}z,}\\ \text{dn}(u,k) & = & \frac{{(\wp (z)-{e}_{2})}^{1/2}}{{(\wp (z)-{e}_{3})}^{1/2}}\\ & = & \frac{\sigma ({\omega }_{2}-z)\sigma ({\omega }_{3})}{\sigma ({\omega }_{3}-z)\sigma ({\omega }_{1})}{e}^{-{\eta }_{3}z+{\eta }_{2}z}.\end{array}\end{eqnarray} Dabei ist \({\eta }_{i}:=\zeta ({\omega }_{i})\) und ζ die Weierstraßsche ζ-Funktion. Die Vorzeichen der Wurzeln sind hierbei durch die angegebenen Gleichungen bereits definiert. Diese Ausdrücke, die zuweilen auch als Definition der Jacobischen elliptischen Funktionen verwendet werden, haben auch den Vorteil, für komplexe Moduln κ anwendbar zu sein.

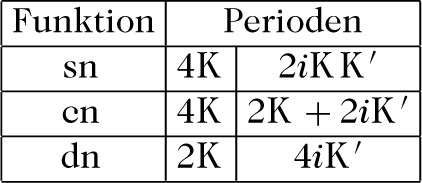
Perioden, Nullstellen und Pole der Jacobischen elliptischen Funktionen findet man gemäß der Definition durch das Argand-Diagramm. Hier eine Zusammenfassung der Perioden in Tabellenform:

Die Nullstellen der Jacobi-Funktionen liegen wie folgt \((n,m\in {\mathbb{Z}})\):

Die folgende Tabelle gibt Aufschluß über die Pole und die Residuen an diesen Polen:

Die Jacobischen Funktionen sn, cn und dn erfüllen auch untereinander einfache Relationen. Am einfachsten sieht man dies in der Darstellung als Umkehrfunktionen elliptischer Integrale: \begin{eqnarray}\begin{array}{l}\begin{array}{ll}{\text{cn}}\,^{2}+{\text{sn}}\,^{2}=1, & {\text{dn}}\,^{2}+{\kappa }^{2}{\text{sn}}\,^{2}=1\end{array}\\ {\text{dn}}^{2}-{\kappa }^{2}{\text{cn}}^{2}={{\kappa }{^{\prime} }}^{2}\\ \begin{array}{ll}{\text {sn}}\,{^{\prime} }={\text {cn dn}}, & {\text {cn}}\,{^{\prime} }={-\text {sn dn}}\end{array}\\ \text d{\text n}\,{^{\prime} }=-{\kappa }^{2}\text{sn cn}\text{.}\end{array}\end{eqnarray} Quadriert man nun die letzten drei Beziehungen, so erhält man die Differentialgleichungen der Jacobischen elliptischen Integrale: \begin{eqnarray}\begin{array}{rll}{\text {sn}}\,{^{\prime {2}} } & = & (1-{\text{sn}}^{2})(1-{\kappa }^{2}{\text{sn}}\,^{2}),\\ {\text {cn}}\,{^{\prime{2}} } & = & (1-{\text{cn}}\,^{2})({\kappa }^{2}{\text{cn}}\,^{2}+{{\kappa }{^{\prime} }}^{2}),\\ {\text {dn}}\,{^{\prime{2}} } & = & (1-{\text{dn}}\,^{2})({\text{dn}}\,^{2}-{{\kappa }{^{\prime} }}^{2}),\\ {\text {sn}}\,{^{\prime\prime} } & = & -\text{sn}\,({\text{dn}}^{2}+{\kappa }^{2}{\text{cn}}\,^{2}),\\ {\text {cn}}\,{^{\prime\prime} } & = & -\text{cn}\,({\text{dn}}^{2}-{\kappa }^{2}{\text{sn}}\,^{2}),\\ {\text {dn}}\,{^{\prime\prime} } & = & -{\kappa }^{2}\text{dn}({\text{cn}}\,^{2}-{\text{sn}}\,^{2}).\end{array}\end{eqnarray}

Die Additionstheoreme für die Jacobischen elliptischen Funktionen erhält man z. B. aus den Additionstheoremen der Weierstraßschen ℘-Funktion. So gilt: \begin{eqnarray}\begin{array}{lll}\text{sn}\,(u+v) & = & =\frac{\text{sn}\,u\,\cdot\, \text{cn}\,v\,\cdot\, \text{dn}\,v+\text{sn}\,v\,\cdot\, \text{cn}\,u\,\cdot\, \text{dn}\,u}{1-{\kappa }^{2}{\text{sn}}\,^{2}u\,\cdot\, {\text{sn}}^{2}v},\\ \text{cn}\,(u+v) & = & =\frac{\text{cn}\,u\,\cdot\, \text{cn}\,v\,-\,\text{sn}\,u\,\cdot\,\text{dn}\,u\,\cdot\, \text{sn}\,v\,\cdot\, \text{dn}\,v}{1-{\kappa }^{2}{\text{sn}}\,^{2}u\,\cdot\, {\text{sn}}\,^{2}v},\\ \text{dn}(u+v) & = & =\frac{\text{dn}\,u\,\cdot\, \text{dn}\,v\,-\,{\kappa }^{2}\text{sn}\,u\,\cdot \text{cn}\,u\,\cdot\, \text{sn}\,v\,\cdot\, \text{cn}\,v}{1-{\kappa }^{2}{\text{sn}}\,^{2}u\,\cdot\, {\text{sn}}\,^{2}v}.\end{array}\end{eqnarray} Im allgemeinen läßt sich jede Jacobische elliptische Funktion pq (u + v) durch eine rationale Funktion in pq (u) und pq (v) ausdrücken. Spezialfälle dieser Relationen sind die Verdoppelungsformeln: \begin{eqnarray}\begin{array}{lll}\text{sn}\,2u & = & 2\frac{\text{sn}\,u\,\cdot\, \text{dn}\,u\,\cdot\, \text{dn}\,u}{1-{\kappa }^{2}{\text{sn}}\,^{4}u}\\ & = & 2\frac{\text{sn}\,u\,\cdot\, \text{cn}\,u\,\cdot\, \text{dn}\,u}{{\text{cn}}\,^{2}u\,+\,{\text{sn}}\,^{2}\,u\,\cdot\, {\text{dn}}\,^{2}u},\\ \text{cn}\,2u & = & \frac{{\text{cn}}\,^{2}u\,-\,{\text{sn}}\,^{2}u\,\cdot\, {\text{dn}}\,^{2}u}{1\,-\,{\kappa }^{2}{\text{sn}}\,^{4}u}\\ & = & \frac{{\text{cn}}^{2}u\,-\,{\text{sn}}\,^{2}\,u\,\cdot\, {\text{dn}}\,^{2}u}{{\text{cn}}\,^{2}u\,+\,{\text{sn}}\,^{2}\,u\,\cdot\, {\text{dn}}\,^{2}u},\\ \text{dn}\,2u & = & \frac{{\text{dn}}\,^{2}u\,-\,{\kappa }^{2}{\text{sn}}\,^{2}\,u\,\cdot\, {\text{cn}}\,^{2}u}{1-{\kappa }^{2}{\text{sn}}\,^{4}u}\\ & = & \frac{{\text{dn}}^{2}u\,+\,{\text{cn}}\,^{2}u({\text{dn}}\,^{2}u\,-\,1)}{\text {dn}^{2}u\,-\,{\text{cn}}\,^{2}u({\text{dn}}^{2}u\,-\,1)}\end{array}\end{eqnarray} In den Spezialfällen κ² = 0 oder κ² = 1 erhält man die gewöhnlichen trigonometrischen oder hyperbolischen Funktionen:

[1] Abramowitz, M.; Stegun, I.A.: Handbook of Mathematical Functions. Dover Publications, 1972.
[2] Erdélyi, A.: Higher Transcendential Functions, vol. 2. McGraw-Hill, 1953.
[3] Tricomi, F.: Elliptische Funktionen. Akadem. Verlagsgesellschaft Leipzig, 1948.