Strahldurchrechnung, 1) trigonometrische S., Verfahren des Optikrechnens zur Bestimmung des Verlaufs und der Aberrationen von meridionalen Strahlen bei der optischen Abbildung durch ein optisches System. Dabei werden sukzessive für alle brechenden Flächen i mit den Radien r_i aus den Schnittweiten

_i und den axialen Strahlneigungen σ_i im Objektraum zunächst die Einfallswinkel

und danach über das Brechungsgesetz die Ausfallswinkel

berechnet (n_i und n'_i Brechzahlen im Objekt- und Bildraum). Daraus resultieren die bildseitigen Strahlneigungen σ

=σ_i+ε_i-ε

, die zusammen mit den ε

die Bildraumschnittweiten

bestimmen. Für die paraxiale Abbildung reduziert sich die trigonometrische S. an den einzelnen Flächen auf die Beziehung


.

Der Übergang zur nächsten, im Abstand d

liegenden Fläche i+1 erfolgt mit den Relationen

und

. Alle von den Flächenscheiteln nach rechts verlaufenden Schnittweiten, Radien und Abstände sowie alle von der optischen Achse orthogonal nach oben verlaufenden Höhen werden positiv gerechnet (Abb.). Optikmodellierung.

2) vektorielle S., in der elektronischen Datenverarbeitung verwendetes Verfahren des Optikrechnens zur Bestimmung des Verlaufs und der Aberrationen windschiefer Strahlen bei der optischen Abbildung durch ein optisches System, für dessen Flächen sukzessive mit Hilfe des vektoriellen Brechungsgesetzes n'(s'×n) = n(s×n) aus den Einheitsvektoren s, s' in der jeweiligen Strahlrichtung und der Flächennormalen im Strahleinfallspunkt und den Objekt- und Bildraumbrechzahlen n und n' die bildseitigen Strahlrichtungseinheitsvektoren

berechnet werden. Raytracing.

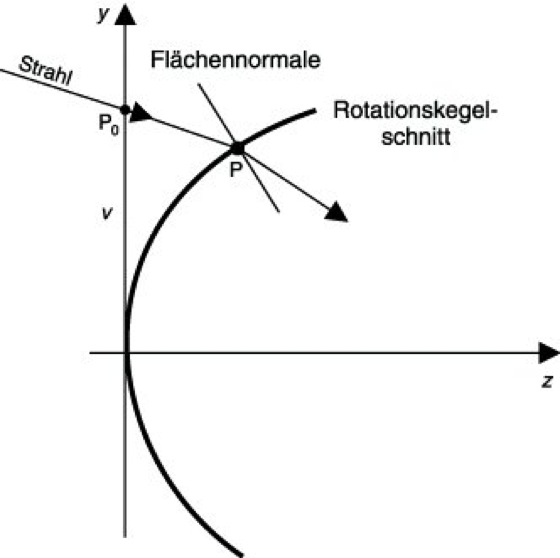
3) S. durch Asphären, die geometrisch-optische Durchrechnung eines Lichtstrahls durch eine oder mehrere asphärische Flächen. Wenn ein einfallender Lichtstrahl, definiert durch einen Punkt auf dem Strahl und durch die Strahlrichtung, gegeben ist, wird sein Verlauf von Fläche zu Fläche bis zum Austritt bestimmt. Diese Durchrechnung verläuft bei jeder Fläche in zwei Stufen: 1. Bestimmung des Schnittpunkts P von Strahl und Fläche (Abb. 2 bis 4). 2. Bestimmung der Strahlrichtung nach Passieren der Fläche (dargestellt in Abb. 2). Der Lichtstrahl kann auch windschief sein.

In der ersten Stufe wählt man meist den Schnittpunkt P₀ des Lichtstrahls mit der Scheitelebene der zu passierenden Fläche als Ausgangspunkt für die Schnittpunktbestimmung. Der Lichtstrahl ist dann gegeben durch die kartesischen Koordinaten u, v, 0 von P₀ und die Strahlrichtungskosinus (L, M, N). Die Koordinaten x, y, z des gesuchten Schnittpunkts P werden dann so bestimmt, daß sie sowohl die linearen Lichtstrahlgleichungen x=u+(L/N)z, y=v+(M/N)z als auch die Gleichung der Asphäre erfüllen. Wenn letztere ein Rotationskegelschnitt ist (Abb. 2), bedeutet das die Lösung einer quadratischen Gleichung, ähnlich wie im Fall einer Sphäre (b=0). Bei allgemeineren Asphären dagegen (Abb. 3 und 4) ist eine Gleichung höheren Grades zu lösen, was im allgemeinen nur iterativ möglich ist. Dies kann z.B. nach dem Newtonschen Näherungsverfahren erfolgen, oder es kann in der in Abb. 3 oder 4 dargestellten Reihenfolge geschehen.

Die zweite Stufe, die Bestimmung der Strahlrichtung nach Passieren der Fläche, erfolgt wie bei sphärischen Flächen durch Anwendung des Brechungs- bzw. Reflexionsgesetzes, nachdem die Richtung der Flächennormale im Schnittpunkt, gekennzeichnet durch ihre Richtungkosinus (L_F, M_F, N_F), bestimmt worden ist. Diese erhält man bei einer allgemeinen Asphäre mit der Gleichung F(x, y, z)=0 durch partielle Differentiationen:

Wenn der Strahlverlauf in dieser Weise bis in den Bildraum bestimmt worden ist, lassen sich seine Aberrationen (auch die Wellenaberration) berechnen.

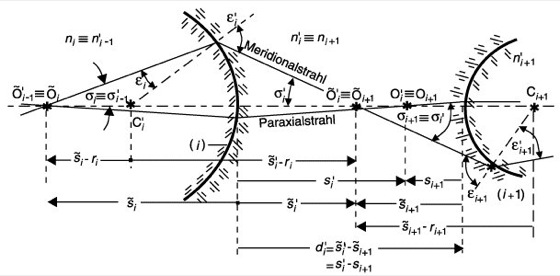
Strahldurchrechnung 1: Zur trigonometrischen Strahldurchrechnung. C Krümmungsmittelpunkt, r Krümmungsradius,

Schnittweiten mit n Brechzahl.

Strahldurchrechnung 2: Durchrechnung eines Lichtstrahls durch einen Rotationskegelschnitt.

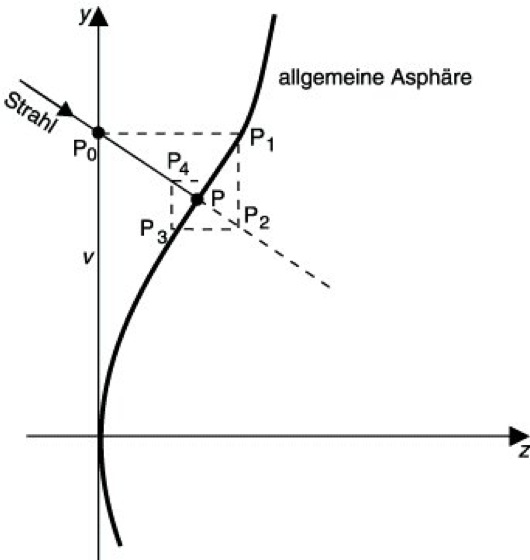
Strahldurchrechnung 3: Bestimmung des Schnittpunkts eines Lichtstrahls mit einer allgemeineren Asphäre. Es werden der Reihe nach die Punkte P₁, P₂, P₃, ... bestimmt, die dem gesuchten Schnittpunkt P beliebig nahe kommen. Die Punkte P₀, P₂, P₄, ... liegen auf dem Strahl, P₁, P₃, P₅, ... auf der Asphäre. P_2k+1 hat dieselben x- und y-Koordinaten wie P_2k. P_2k+2 hat dieselbe z-Koordinate wie P_2k+1(k = 0, 1, 2, ...). (Nach: G. Schulz, Aspheric Surfaces, in: Progr. in Optics XXV, 1988.).

Strahldurchrechnung 4: Schnittpunktbestimmung ähnlich wie in Abb. 3, nur ist der Punkt P_2k+2 der Schnittpunkt des Strahls mit der Tangentialebene an die Asphäre im Punkt P_2k+1(k = 0, 1, 2, ...). (Nach: G. Schulz, Aspheric Surfaces, in: Progr. in Optics XXV, 1988.).