Hemmes mathematische Rätsel: Wie lässt sich die Größe des Winkels bestimmen?
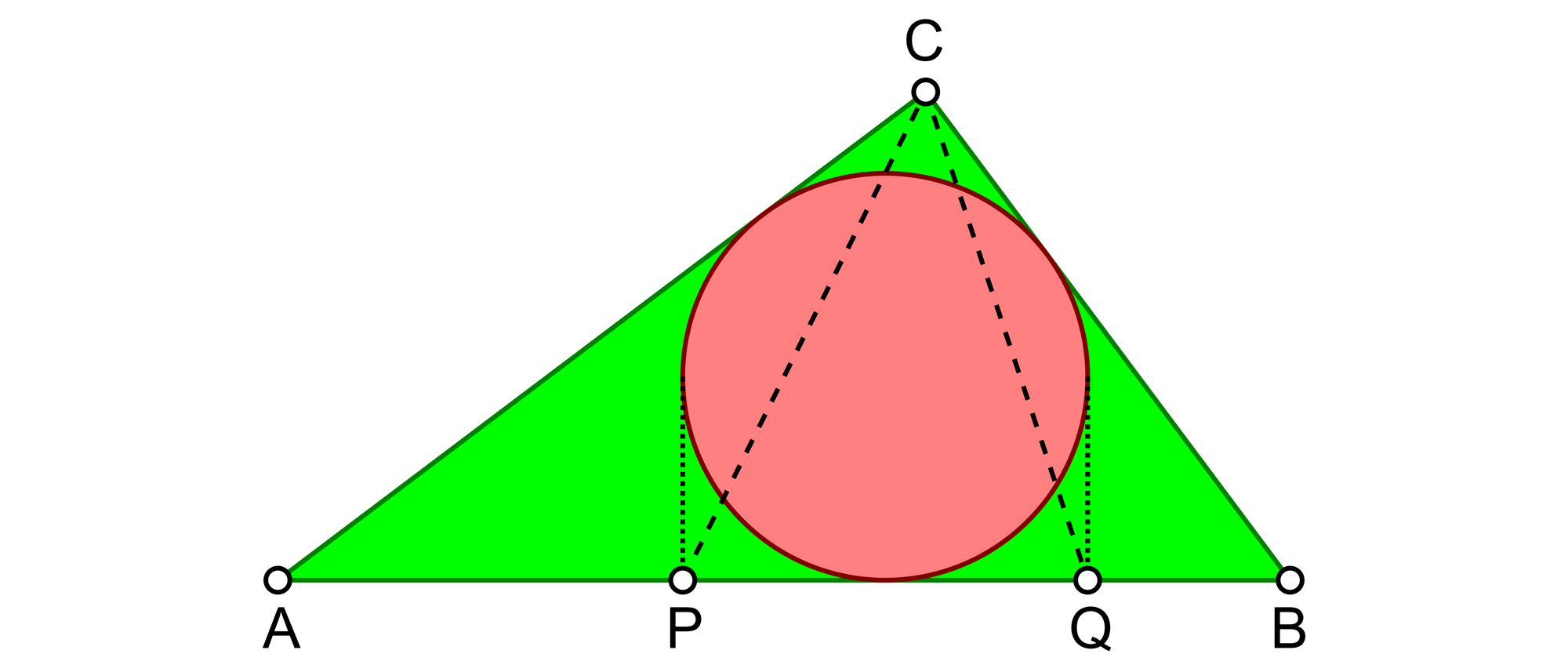
Die Strecke PQ ist die Projektion des Inkreises eines rechtwinkligen Dreiecks ABC auf die Hypotenuse AB. Wie groß ist der Winkel PCQ?
Ist M der Mittelpunkt des Inkreises, so sind die beiden Dreiecke MRP und CTM deckungsgleich. Folglich ist MC = MP. Analog dazu ist MC = MQ. Damit ist M auch der Mittelpunkt des Umkreises des Dreiecks QCP. Da die beiden Dreiecke MRP und QSM rechtwinklig und gleichschenklig sind, hat der Winkel PMQ eine Größe von 90°. Er ist der Mittelpunktswinkel über die Umkreissehne PQ. Hingegen ist der Winkel PCQ ein Umfangswinkel über diese Sehne und deshalb halb so groß. Folglich hat der Winkel PCQ eine Größe von 45°.
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Welche sechsstelligen Zahlen sind gesucht?
- Wie groß ist die Fläche des Trapezes?
- Wie können die Zahlen noch verteilt werden?
- Warum stimmt diese Aussage?
- Wie lang ist die Sehne des Kreises?
- Welche Zahl fehlt?
- Wie kann das Rätsel gelöst werden?
- Wie viele dieser Zahlen gibt es?
- Wie viel deckt das Quadrat ab?
- Wie muss das Streichholz umgelegt werden?
- Welche Uhrzeit ist gesucht?
- Wie viel Prozent decken die Preise ab?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Schreiben Sie uns!
1 Beitrag anzeigen