Lexikon der Mathematik: Modulfunktion
gelegentlich auch modulare Funktion genannt, eine in der oberen Halbebene \({\mathcal{H}}\) ={ z ∈ ℂ : Im z > 0 } meromorphe Funktion f derart, daß eine Untergruppe \({\mathcal{G}}\) der Modulgruppe Γ existiert mit f(M(z)) = f(z) für alle \({z \in \mathcal{H}}\) und alle \({M \in \mathcal{G}}\).
Offensichtlich ist jede konstante Funktion eine Modulfunktion. Es ist nicht ganz einfach, eine nichtkonstante Modulfunktion zu konstruieren. Dies wird im folgenden an einem der wichtigsten Beispiele demonstriert. Man startet mit dem Gebiet
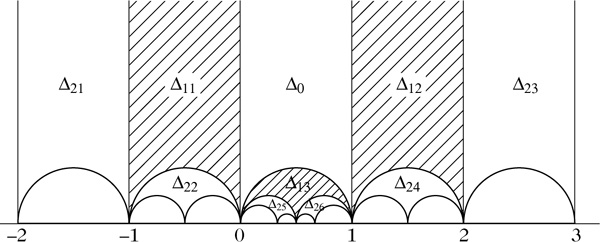
Dies ist ein sog. Kreisbogendreieck mit den Ecken 0, 1 und ∞. Dieses Dreieck wird an seinen drei Seiten gespiegelt, wodurch die Kreisbogendreiecke Δ11, Δ12 und Δ13 entstehen. Nun wird jedes dieser Dreiecke an den beiden Seiten, die nicht auch Seiten von Δ0 sind, gespiegelt. Hierdurch entstehen sechs weitere Dreiecke. So fährt man fort. Vereinigt man alle entstehenden Dreiecke und nimmt noch deren Seiten ohne die Punkte auf der reellen Achse hinzu, so erhält man die gesamte obere Halbebene \({\mathcal{H}}\). Insgesamt entsteht also eine „Pflasterung“ von \({\mathcal{H}}\), die man auch Modulnetz nennt.
Modulnetz
Zur Konstruktion einer Modulfunktion wählt man nun eine konforme Abbildung f0 von Δ0 auf \({\mathcal{H}}\). Diese läßt sich zu einem Homöomorphismus von \({\bar{\Delta }}_{0}\) auf \(\bar{\mathcal{H}}\) fortsetzen. Wählt man f0 noch so, daß f0(∞) = 0, f0(0) = 1 und f0(1) = ∞, so ist f0 eindeutig festgelegt. Mit Hilfe des Schwarzschen Spiegelungsprinzips kann f0 zu einer in dem Gebiet \(({\bar{\Delta }}_{0}\backslash \{0,\,1\})\cup {\Delta }_{11}\cup {\Delta }_{12}\cup {\Delta }_{13}\) holomorphen Funktion f1 fortgesetzt werden. Durch f1 wird jedes der Dreiecke Δ11, Δ12, Δ13 konform auf die untere Halbebene { z ∈ ℂ : Im z < 0 } abgebildet. Durch sukzessive weitere Spiegelung wie oben beschrieben wird schließlich f0 zu einer eindeutig bestimmten in \({\mathcal{H}}\) holomorphen Funktion λ fortgesetzt. Bezeichnet Γ0 die von den Matrizen
erzeugte Untergruppe von Γ, so kann man zeigen, daß λ eine Modulfunktion bezüglich Γ0 ist. Die Gruppe Γ0 besteht aus allen Möbius-Transformationen
in Γ derart, daß a, d ungerade und b, c gerade ganze Zahlen sind.
Ähnlich wie bei der vollen Modulgruppe existiert auch ein Fundamentalbereich von Γ0. Dieser wird gegeben durch die Menge
Dann gilt
und M(\({\mathcal{F}}\)0) ∩ N(\({\mathcal{F}}\)0) = ∅ für alle M, N ∈ Γ0 mit M ≠ N. Weiter ist die Menge { M(0) : M ∈ Γ0 } dicht in ℝ.
Man nennt λ auch die Modulfunktion. Weitere wichtige Eigenschaften von λ sind:
- Es gilt λ′(z) ≠ 0 für alle \({z \in \mathcal{H}}\).
- Es gilt λ(\({\mathcal{H}}\)) = ℂ0,1 := ℂ \{0, 1}.
- Es ist \({\mathcal{H}}\) das Holomorphiegebiet von λ.
- Es ist λ: \({\mathcal{H}}\) → ℂ0,1 eine Überlagerungsabbildung, d. h. zu jedem w0 ∈ ℂ0,1 gibt es eine offene Umgebung U ⊂ ℂ0,1 von w0 derart, daß jede Zusammenhangskomponente des Urbilds λ−1(U) ⊂ \({\mathcal{H}}\) durch λ konform auf U abgebildet wird.
Mit Hilfe der Modulfunktion λ kann ein sehr eleganter Beweis des großen Satzes von Picard geführt werden.
Mit dem oben beschriebenen Spiegelungsverfahren kann man ebenfalls Modulfunktionen bezüglich der vollen Modulgruppe Γ konstruieren. Hierdurch erhält man z. B. die sog. J-Funktion mit folgenden Eigenschaften:
- Es ist J eine in \({\mathcal{H}}\) holomorphe Funktion mit J(\({\mathcal{H}}\)) = ℂ.
- Das Kreisbogendreieck
\begin{eqnarray}{\Delta }^\prime\,:\,=\,\{z\,\in \,\mathca{H}\,:\,-\frac{1}{2}\,\lt \,\text{Re}\,z\,\lt \,0,\,|z|\,\gt \,1\}\end{eqnarray} wird durch J konform auf \({\mathcal{H}}\) abgebildet. - Es gilt J(∞) = ∞, J(ϱ) = 0 und J(i) = 1, wobei ϱ derjenige Randpunkt von Δ′ mit \(\text{Re}\,\varrho \,=\,-\frac{1}{2}\) und |ϱ|= 1 ist.
Die J-Funktion ist über die Gleichung
Eine weitere wichtige Modulfunktion bezüglich Γ ist die j-Funktion. Für sie gilt
Durch j wird das Kreisbogendreieck
konform auf \({\mathcal{H}}\) abgebildet, und es gilt j(∞) = ∞, j(i) = 0 und j(−ϱ2) = 27. Offensichtlich ist die Menge aller Modulfunktionen bezüglich der vollen Modulgruppe Γ ein Körper, den man mit K(Γ) bezeichnet, und der den Körper ℂ der komplexen Zahlen als Unterkörper enthält. Genauer gilt K(Γ) = ℂ(j), d. h. zu jeder Modulfunktion f ∈ K(Γ) existiert eine rationale Funktion R mit f = R ∘ j.
Die Theorie der Modulfunktionen kann in gewissem Sinne als Erweiterung der Theorie der elliptischen Funktionen aufgefaßt werden, wobei die Rolle des Periodenparallelogramms von dem Modulnetz übernommen wird. Die oben behandelten Modulfunktionen können auch mit Hilfe der Weierstraßschen ℘-Funktion definiert werden.
Schreiben Sie uns!