Wahrscheinlichkeitsnetz, in Form einer Netzstruktur eingerichtetes Spezialpapier, welches in der deskriptiven Statistik zur graphischen Überprüfung der Hypothese verwendet wird, daß die unbekannte Verteilung einer Zufallsgröße X einer Normalverteilung N(μ, σ²) unterliegt.

Das Wahrscheinlichkeitspapier ist so eingerichtet, daß sich bei Einzeichnen der kumulierten Wahrscheinlichkeiten F(x) einer beliebigen Normalverteilung eine Gerade ergibt. Die Ordinaten- werte des Netzes sind die Summenhäufigkeitsprozente von 0, 01 bis 0, 99. Die Abzisse kann linear (in Millimetern) oder logarithmisch eingeteilt sein. Im letzteren Fall spricht man von logarithmischem Wahrscheinlichkeitspapier. Dieses wird zum Prüfen des Vorliegens einer Lognormalverteilung verwendet.

Es sei X eine Zufallsgröße, die auf Normalverteilung geprüft werden soll, und sei (x₁, …, x_n) eine Stichprobe von X. Man berechnet zunächst die empirische Verteilungsfunktion F_n(x) der Beobachtungsdaten an jeder Stelle x_i, i = 1, …, n. Anschließend trägt man die Punkte (x_i, F_n(x_i)) für i = 1, …, n auf dem Wahrscheinlichkeitspapier ab. Ist X normalverteilt, so werden die Punkte (x_i, F_n(x_i)), i = 1, …, n annähernd auf einer Geraden liegen.

Ebenfalls kann man mit dem Wahrscheinlichkeitspapier die Varianz Var(X) und den Erwartungswert EX einer normalverteilten Zufallsgröße schätzen. Eine Schätzung \begin{eqnarray}\overline{{x}_{g}}\end{eqnarray} für EX ist der Abszissenwert des Schnittpunktes der durch (x_i, F_n(x_i)), i = 1, …, n gebildeten Geraden mit der Waagerechten y = 0, 5. Bringt man ferner die Waagerechten y = 0, 16 und y = 0, 84 in Schnitt mit der eingezeichneten Geraden und lotet sie auf die x-Achse, so kann man die Punkte \begin{eqnarray}\overline{{x}_{g}}+{s}_{g}\end{eqnarray} und \begin{eqnarray}\overline{{x}_{g}}-{s}_{g}\end{eqnarray} auf der x-Achse ablesen. Die Schätzung s_g für die Standardabweichung \begin{eqnarray}\sqrt{Var(X)}\end{eqnarray} von X ergibt sich dann durch Bildung der Differenz beider Werte und Division durch 2.

Die Prüfung einer Normalverteilung mit Hilfe des Wahrscheinlichkeitspapiers gibt einen guten Überblick, ist aber sehr ungenau und in jedem Fall durch einen entsprechenden Hypothesentest, z. B. den χ²-Anpassungstest für Verteilungsfunktionen oder den Kolmogorow-Smirnow-Test, zu ergänzen. Andere graphische Methoden der Verteilungsprüfung sind der P-P-Plot und der Q-Q-Plot.

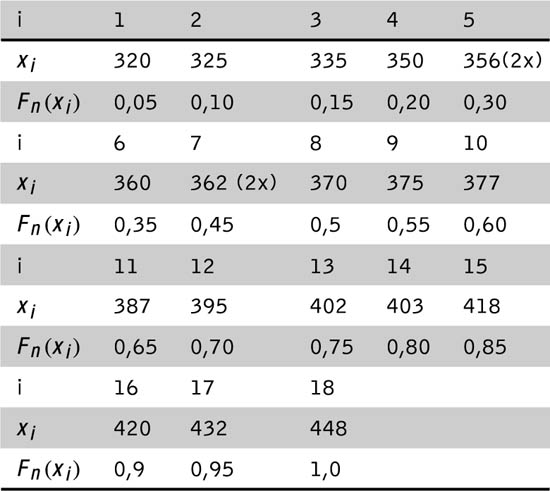
Ein Beispiel. Die Ermittlung von Durchlaufzeiten von Werkstücken durch ein Fertigungssystem ergab (in geordneter Reihenfolge) folgende 20 Werte (in Minuten):

Die Abbildung zeigt die Punkte (x_i, F_n(x_i)) im Wahrscheinlichkeitsnetz.

Als grobe Schätzungen \begin{eqnarray}\overline{{x}_{g}}\end{eqnarray} und s_g für Erwartungswert und Varianz der zufälligen Durchlaufzeit X liest man aus der Abbildung \begin{eqnarray}\overline{{x}_{g}}=370\end{eqnarray} und \begin{eqnarray}{s}_{g}=\frac{(\overline{{x}_{g}}+{s}_{g})-(\overline{{x}_{g}}-{s}_{g})}{2}=\frac{406-337}{2}=34,5\end{eqnarray} ab. Die Werte entsprechen in diesem Fall annähernd denjenigen, die man durch Interpolation aus der Tabelle erhalten würde.