Die Lapse-Funktion ist eine Größe in der Allgemeinen Relativitätstheorie (ART), die gravitativ bedingte Dehnung der Zeit mathematisch darstellt. Die Lapse-Funktion hängt von den Koordinaten ab, also wo sie genau in der Raumzeit ausgewertet wird.

Achtung bei Begrifflichkeiten

Die ART bietet eine ganze Palette von Rechengrößen, die diesen physikalischen Zeitdehnungseffekt verdeutlichen. Man muss dabei nur sehr genau aufpassen, wie die jeweilige Größe definiert ist. Zur Lapse-Funktion α kann man auch Rotverschiebung oder Rotverschiebungsfaktor (oft g-Faktor genannt) sagen; aber man sollte sich über die subtilen Unterschiede in der mathematischen Berechnung im Klaren sein. Die kosmologische Rotverschiebung z hat eine physikalisch andere Ursache (nämlich eine Expansion der Raumzeit), aber dennoch ist auch dieses z mit einem Zeitdehnungseffekt assoziiert: die Uhren entfernter Supernovae ticken anders als lokale Uhren.

Lapse in flacher vs. gekrümmten Raumzeit

Betrachten wir zunächst nur den Grenzfall der Speziellen Relativitätstheorie. Hier wird die Raumzeit durch die Minkowski-Geometrie beschrieben. Die Lapse-Funktion ist überall exakt 1, weil die Raumzeit flach ist. Das gilt auch bei gekrümmten Raumzeiten, in dem Gebiet, wo sie asymptotisch flach sind. Alle klassischen Schwarzen Löcher der ART sind asymptotisch flach; nähert man sich allerdings der Krümmungssingularität, so nimmt die Krümmung zu und auch die Lapse-Funktion verändert sich.

Definition und Veranschaulichung

Die allgemeine Definition ist im Prinzip die Ableitung der Eigenzeit τ nach der Koordinatenzeit t. Dies entspricht einem Vergleich des Gangs der Uhr eines relativ ruhenden Beobachters, des FIDO (engl. fiducial observer), mit einem Beobachter im Unendlichen.
Die Bezeichnung Lapse kommt aus dem Englischen: to lapse heißt 'verfließen' oder 'verzögern'. Die Lapse-Funktion ist gerade ein Maß dafür, um welchen Faktor die beiden Uhren verschieden gehen. Denn aufgrund der gravitativen Zeitdilatation messen frei fallender und entfernter, ruhender Beobachter unterschiedliche Zeitmaße.

Beispiel: Kerr-Geometrie

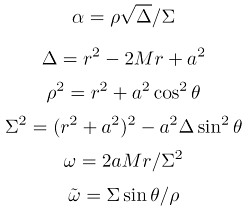Betrachten wir als Beispiel die Kerr-Metrik, die die gekrümmte Raumzeit rotierender Massen relativistisch beschreibt. Wir verwenden die Boyer-Lindquist-Form der Kerr-Lösung. Hier ist die 00-Komponente des kontravarianten metrischen Tensors gerade das negative, inverse Quadrat der Lapse-Funktion α (Signatur der Metrik sei – + + +).

Bezug zu zerlegten Raumzeiten

Im ADM-Formalismus oder 3+1 Split wird die vierdimensionale Raumzeit in Hyperflächen zerlegt (Foliation). Diese Hyperflächen sind dreidimensionale, rein räumliche Unterräume, auf denen die Zeit jeweils konstant ist. Die Lapse-Funktion gibt nun an, wie sich der Zeitablauf von einer Hyperfläche zur nächsten verändert. Mit der allgemeinen Formel des 3+1 Split einer gesplitteten Metrik lassen sich Lapse-Funktion und Shift-Vektor für jede beliebige Metrik beschaffen.

Visualisierung der Lapse-Funktion

Die Lapse-Funktion eignet sich gut zur Visualisierung des Gravitationstrichters, wie die Abbildung oben zeigt. Am Ereignishorizont verschwindet die Lapse-Funktion in Boyer-Lindquist-Koordinaten: Die Gravitationsrotverschiebung wird unendlich – das ist allerdings nur ein Folge der Koordinatensingularität, also unzureichender Koordinaten. An den Rändern der Raumzeit (Radialkoordinate r gegen +∞) wird die Lapse-Funktion eins und die Raumzeit asymptotisch flach: In der Fernzone sind Gravitationsquellen 'minkowskisch'.